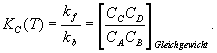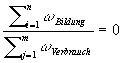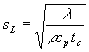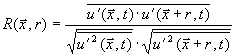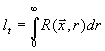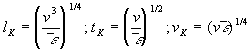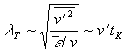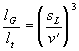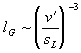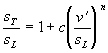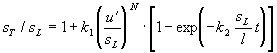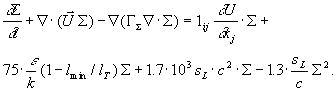zurück zur Startseite
3 Ottomotoren
3.3 Ottomotorische Verbrennung
3.3.1 Grundlagen
der ottomotorischen Verbrennung
Im modernen Ottomotor mit Saugrohreinspritzung sind
Kraftstoff und Luft untereinander und mit dem im Zylinder verbleibenden Restgas während des Ansaugvorgangs und der anschließenden
Kompression bereits weitgehend gasförmig gemischt, so daß
unter normalen Bedingungen vor Beginn der Zündung ein homogenes Gemisch
vorliegt. In diesem Abschnitt soll daher nur die Verbrennung in homogenen
Gemischen betrachtet werden. Ottomotoren mit geschichteter Mischung durch
Direkteinspritzung sind Gegenstand aktueller Forschung, die hier nicht
referiert werden soll.
Nach der Zündung, die zum Ende des Kompressionsvorgangs ca.
25 Grad Kurbelwinkel vor dem oberen Totpunkt stattfindet, bildet sich zunächst
ein laminarer Flammenkern aus, der sehr schnell turbulent wird. Dieser
entwickelt sich zu einer turbulenten Flammenfront, die sich zunächst
kugelförmig ausbreitet, bis sie die Brennraumwände am Kolben, Zylinderkopf und
am Zylinder erreicht hat. Da der Abstand zwischen Kolben und Zylinderkopf beim
klassischen Zweiventilmotor wesentlich kleiner ist als der Bohrungsdurchmesser
des Zylinders, ist der Brennraum nahezu scheibenförmig und die
Flammenausbreitung kann, ausgehend von der seitlich angeordneten Zündkerze als
nahezu zweidimensional angesehen werden. Bei Vierventilmotoren, die eine
zentral im Zylinderkopf liegende Zündkerze besitzen, ist die Flammenausbreitung
wegen der zeltförmigen Brennraumgeometrie über eine längere Strecke kugelförmig
und erreicht erst später den Kolben und die Zylinderwand. In Abbildung 3.3-1 ist der Ausbreitungsvorgang
anhand von Schlierenaufnahmen in einem
scheibenförmigen Brennraum eines 1.6 l Vierzylinder VW-Transparentmotors bei
2000 U/min dargestellt, der im Teilprojekt A2 verwendet wurde. Der Motor
unterscheidet sich von der Serienversion im wesentlichen durch verlängerte Kolben sowie ein
Zwischengehäuse zur entsprechenden Verlängerung der Zylinder. Der verlängerte
Kolben ist mit einem Quarzfenster im Kolbenboden ausgerüstet und weist
seitliche Langloch-Öffnungen auf, denen entsprechende Öffnungen in den
verlängerten Zylindern des Zwischengehäuses gegenüberstehen. Diese Öffnungen
ermöglichen bei laufendem Motor das Einschieben eines 45°-Spiegels, über
welchen die Vorgänge im Brennraum durch das Kolbenfenster beobachtet werden
können. Die Zündung erfolgt bei 40 Grad Kurbelwinkel vor dem oberen Totpunkt.
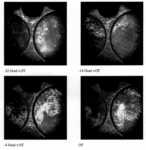
Abbildung 3.3-1: Schlierenaufnahmen
der Flammenausbreitung im Transparentmotor
Ausgehend von der Zündkerze, die innerhalb der als dunkler
Halbkreis sichtbaren Bohrung im oberen Teil der Bilder liegt, entwickelt sich
eine turbulente Flammenfront, die im ersten Bild bei -22 Grad Kurbelwinkel vor
OT zum ersten Mal sichtbar wird. Sie entwickelt sich weiter, wobei bei -14 Grad
vor OT große turbulente Strukturen sichtbar werden. Das Gebiet der
aufgefalteten Flammenfront ist aufgrund der dort vorliegenden großen
Dichtegradienten in den Schlierenaufnahmen als heller
Bereich sichtbar. Bei -4 Grad vor OT erscheint hinter der Front wieder ein
dunklerer Bereich, der das verbrannte Gemisch darstellt. Beim oberen Totpunkt
hat die Flammenfront den überwiegenden Teil der Mischung erreicht.
Zur Beschreibung der turbulenten Flammenausbreitung soll im folgenden auf die Grundlagen der
Reaktionskinetik sowie der Turbulenz eingegangen und sodann die
Schadstoffbildung im Ottomotor behandelt werden. Untersuchungen zur Interaktion
zwischen Turbulenz und Kinetik, die die Struktur der turbulenten Flamme
bestimmen, sind in den Teilprojekten A2 und A5 des Sonderforschungsbereichs
durchgeführt worden. Die zunächst dargestellten Grundlagen der Reaktionskinetik
sollen auf neuere Arbeiten zur Reaktion chemischer Mechanismen verweisen, in
denen laminare Brenngeschwindigkeiten und Zündverzugszeiten für motorische
Modellkraftstoffe hergeleitet wurden.
3.3.2 Reaktionskinetik
3.3.2.1
Die Reaktionsgeschwindigkeit
Die zentrale Größe der chemischen Kinetik ist die Reaktionsgeschwindigkeit.
Unter der Geschwindigkeit einer homogenen Reaktion versteht man die pro
Volumen- und Zeiteinheit umgesetzte Anzahl von Molen der beteiligten
Komponenten. Die Reaktionsgeschwindigkeit ist eine Funktion des
thermodynamischen Zustandes (Druck und Temperatur), sowie der Moldichten der an
der Reaktion teilnehmenden Komponenten. Unter der Moldichte wird die Anzahl der
Mole einer Komponente pro Volumeneinheit verstanden. Sie ist damit äquivalent
zur Konzentration. Wird beispielhaft eine Elementarreaktion geschrieben als
Gleichung 3.3-1: 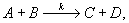
dann ergibt sich die zeitliche Änderung der Moldichte CA der chemischen Komponente A zu
Gleichung 3.3-2: 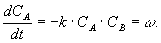
Diese definiert die Reaktionsgeschwindigkeit w.
Der Geschwindigkeitskoeffizient k ist in erster Linie von der Temperatur abhängig (nur in
Sonderfällen auch vom Druck). Der Temperatureinfluß
auf den Geschwindigkeitskoeffizienten wird durch den erweiterten Ansatz von
Arrhenius recht gut wiedergegeben, der in Form geschrieben werden kann
Gleichung 3.3-3: 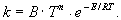
Hierin gibt die Aktivierungsenergie E den Energiebetrag an, der zur Überwindung einer Potentialschwelle
während der Reaktion erforderlich ist.
Eine chemische Elementarreaktion vollzieht sich häufig nach
dem in Gleichung 3.3-1 angegebenen Schema, d.h. zwei
Ausgangsstoffe reagieren zu zwei Reaktionsprodukten. Eine solche Reaktion wird
als bimolekular bezeichnet. Neben bimolekularen Reaktionen laufen aber auch
uni- und trimolekulare Reaktionen ab.
Die Druckabhängigkeit eines Reaktionsvorgangs wird durch den
relativen Einfluß trimolekularer
Reaktionen bestimmt. Für einen höheren Druck steigt die Anzahl der Mole im
Reaktionsvolumen und damit erhöht sich der Einfluß trimolekularer Reaktionen gegenüber bimolekularer
Reaktionen.
Bei vielen Elementarreaktionen muß
neben der angegebenen Vorwärtsreaktion auch die Rückwärtsreaktion
berücksichtigt werden. Statt der Gleichung
3.3-1
schreibt man
Gleichung 3.3-4: 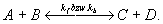
Die Änderung der Moldichte der Komponente A ist dann
Gleichung 3.3-5: 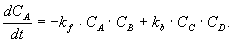
Hier bedeuten kf der Geschwindigkeitskoeffizient der
Vorwärtsreaktion (f für forward) und kb der der Rückwärtsreaktion (b für backward).
Der Quotient aus beiden Geschwindigkeitskoeffizienten gibt die
Gleichgewichtskonstante der Reaktion an
Gleichung 3.3-6: 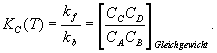
Ist nun bekannt, daß sich eine
Reaktion im partiellen chemischen Gleichgewicht befindet, ist es möglich, die
Konzentration eines Reaktanten mit Hilfe von Gleichung
3.3-6
zu bestimmen, ohne dabei eine Erhaltungsgleichung für die entsprechende
Komponente zu lösen.
3.3.2.2
Stationarität von Zwischenprodukten
Einige sehr reaktive Komponenten haben die Eigenschaft, daß sie nach ihrer Bildung wieder sehr schnell verbraucht
werden. Die Konzentration solcher Komponenten bleibt somit immer klein. Die
Änderung der Konzentration einer Komponente ist generell gegeben durch die
Differenz aller diese Komponenten bildenden und verbrauchenden Reaktionen
Gleichung 3.3-7: 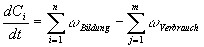
Wenn die Konzentration einer Komponente auf Grund des sehr
viel schnelleren Verbrauchs klein ist gegenüber denjenigen
anderer Komponenten, kann die linke Seite dieser Gleichung vereinfachend
zu null gesetzt werden. Diese Annahme wird als Stationaritätsannahme
bezeichnet. Somit ergibt sich
Gleichung 3.3-8: 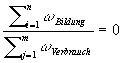
Da die Verbrauchsreaktionen immer proportional zur Moldichte
der verbrauchten Komponente ist (vergl. Gleichung 3.3-2) läßt
sich hieraus die Konzentration der Komponente Ci berechnen.
3.3.2.3
Komplexe Reaktionsschemata
Die Oxidation organischer Verbindungen vollzieht sich in der
Regel in einer Aneinanderreihung einer Vielzahl von chemischen
Elementarreaktionen (Reaktionskette). Im ersten Stadium werden aus den stabilen
Ausgangsstoffen aktive Zwischenprodukte (Radikale) gebildet. Hierbei erfolgt
die Produktion der Zwischenprodukte anfangs sehr langsam, da Reaktionen
stabiler Moleküle untereinander eine hohe Aktivierungsenergie besitzen.
Demgegenüber reagieren die erzeugten Zwischenprodukte sehr schnell mit den
Ausgangsstoffen dank der geringen Aktivierungsenergie der beteiligten
Reaktionen. Es besteht nun die Möglichkeit, daß in
einer Reaktion ein aktives Zwischenprodukt verbraucht wird und zwei oder mehr
durch die Reaktion wieder gebildet werden. In diesem Fall ergibt sich ein
selbstbeschleunigender Reaktionsverlauf (autokatalytisch). Dieses Verhalten
einer Reaktion wird als „kettenverzweigend“ bezeichnet. Analog zu dem
kettenverzweigenden Verhalten ist der entgegengesetzte Verlauf einer Reaktion
möglich, d.h. sie verbraucht mehr aktive Zwischenprodukte als sie bildet. Eine
solche Reaktion wird als „kettenabbrechend“ bezeichnet. Werden in einer
Reaktion soviele aktive Zwischenprodukte verbraucht
wie gebildet, so spricht man von einer „kettenfortpflanzenden“ Reaktion.
Vollständige Reaktionsschemata und relativ genaue kinetische
Daten existieren bereits seit einigen Jahren
[i][1].
Die wichtigste Reaktion des Wasserstoff-Sauerstoff-Systems ist die
Kettenverzweigungsreaktion
1 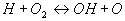 .
.
Hier werden aus einem H-Radikal bei der Reaktion mit dem
stabilen O2-Molekül zwei Radikale, nämlich OH und O gebildet. Diese
werden in den sehr schnellen Austauschreaktionen 2, 3 und 4 untereinander und
in das H-Radikal umgewandelt
2 
3 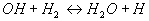
4 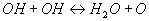 .
.
Aus einem O-Atom werden in Reaktion 2 zwei Radikale, nämlich
H und OH gebildet. Demgegenüber zeigt Reaktion 3, daß
aus einem OH-Radikal wieder ein H-Radikal gebildet wird. In Reaktion 4 wird aus
2 OH-Radikalen ein O-Radikal gebildet. Durch Addition von Reaktion 2 und 4
erhält man Reaktion 3. Die Reaktionen 2, 3 und 4 sind somit „linear abhängig“.
Dies hat für den kinetischen Ablauf keine Bedeutung und spielt erst eine Rolle,
wenn sich das System dem chemischen Gleichgewicht nähert. Der Kettenbruch, d.h.
der Verbrauch der Radikale, erfolgt bei Anwesenheit von Sauerstoff in erster
Linie durch die Reaktion
5 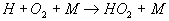 .
.
Reaktion 5 führt zu dem Peroxid-Radikal HO2, das
in den Reaktionen
6 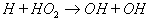
7 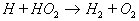
8 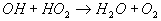
weiter reagiert. Von diesen Reaktionen bewirkt Reaktion 6, daß wieder neue Radikale OH gebildet werden, die z.B. über
Reaktion 3 wieder die in Reaktion 5 und 6 verbrauchten H-Radikale ersetzen.
Diese Reaktion ist also radikal- und damit kettenerhaltend. Parallel zu
Reaktion 6 laufen jedoch immer die Reaktionen 7 und 8 ab, die zum Kettenabbruch
führen. Daher werden in der Summe über den Weg der Reaktion 5 immer Radikale
und damit Kettenträger dem System entzogen.
Es gibt praktisch nur eine wichtige Reaktion, mit der in
technischen Systemen CO zu CO2 oxidiert wird, nämlich
9 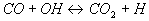 .
.
Dies bedeutet auch, daß reines CO
nur dann hinreichend gut verbrennt, wenn in irgendeiner Form elementarer
Wasserstoff vorhanden ist, so daß OH gebildet werden
kann.
Der einfachste motorische Modellkraftstoff ist Methanol CH3OH.
Im folgenden soll ein stark
verkürzter Mechanismus der Methanoloxidation
betrachtet werden, der als Zwischenprodukt nur CH2OH, CH2O
und CHO enthält. Ein solcher Mechanismus ist bereits imstande, die Oxidation
von Methanol gut zu beschreiben. Bei sehr hohen Temperaturen spielt die
Dissoziation von Methanol zu CH3 und OH und die danach folgende
Rekombination von CH3 + CH3 zu C2H6
und C2H5 + H eine gewisse Rolle. Dadurch ergibt sich eine
Reaktionskette über C2-Kohlenwasserstoffe wie C2H6,
C2H5, C2H4, C2H3,
C2H2 bis zu C2H, die schließlich durch
Rekombination zu weiteren höheren Kohlenwasserstoffen und zur Rußbildung führen
kann. Dieser Reaktionspfad und insbesondere die Rußbildung ist bei Methanol
wesentlich schwächer als bei aliphatischen Kohlenwasserstoffen wie Methan, n-Heptan
oder iso-Oktan, da bei der Methanoloxidation
nur wenig CH3 gebildet wird.
Als Startreaktion kann somit die Dissoziationsreaktion
10 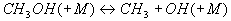
angesehen werden. Reaktion 10 kann sowohl als unimolekulare
Reaktion oder als bimolekulare Reaktion mit dem inerten Stoßpartner M ablaufen.
Sie ist daher druckabhängig. Wenn bereits Radikale vorliegen, wird CH3OH
vor allem durch Reaktionen mit dem OH-Radikal entsprechend
11 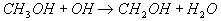
zu CH2OH umgesetzt. Für die Oxidation von CH2OH
zum Formaldehyd CH2O ist das H-Radikal entscheidend
12 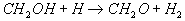 .
.
Vom stabilen Formaldehyd-Molekül CH2O wird ein
weiteres H-Atom durch Reaktionen mit H oder OH abstrahiert
13 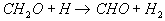
14 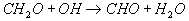 ,
,
wobei das CHO-Radikal gebildet wird. Konkurrierende
Reaktionen mit HO2 und O2 als Reaktionspartner sind hier
unbedeutend. Schließlich wird CHO durch die Reaktionen
15 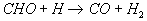
16 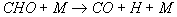
zum stabilen Zwischenprodukt CO umgewandelt.
Selbst ein stark verkürzter Mechanismus, wie ihn die
Reaktionen 1-16 darstellen, beinhaltet offensichtlich eine Reihe von parallelen
und konkurrierenden Reaktionspfaden. Dies darf jedoch nicht darüber
hinwegtäuschen, daß nur sehr wenige
Schlüsselreaktionen den Gesamtablauf wesentlich bestimmen und damit das
Endergebnis beeinflussen. Man nennt diese Reaktionen
„geschwindigkeitsbestimmend“. Es sind diejenigen, die den Verbrauch von CH3OH
und O2 sowie die Oxidation von CO zu CO2 beherrschen,
sowie diejenigen, die als wesentliche Kettenverzweigungs- und
Kettenabbruchreaktionen die Bilanz der Radikale bestimmen. Neben der
wichtigsten Verbrauchsreaktion von Methanol
11 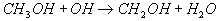
ist dies in erster Linie die Reaktion
9 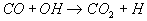 ,
,
durch die das schließlich gebildete CO zum Endprodukt CO2
oxidiert wird.
Ebenso wichtig ist die Kettenverzweigungsreaktion
1 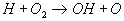 ,
,
die den Sauerstoff O2 verbraucht. Sie hat eine
relativ hohe Aktivierungsenergie, ist also stark temperaturabhängig. Sie muß mit der Reaktion
5 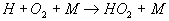
konkurrieren, die einen Kettenabbruch bewirkt. Wenn die
Reaktion 5 schneller abläuft als die Reaktion 1, werden dem System zu viele
Radikale entzogen. Der Kettenabbruch ist dann schneller als die
Kettenverzweigung und die Verbrennung kann nicht aufrechterhalten werden.
3.3.2.4
Reduzierte Mechanismen
Mit den oben eingeführten Stationaritätsannahmen
soll ein Globalmechanismus mit Hilfe von Stationaritätsannahmen
abgeleitet werden. Als Hauptkette für die Methanol-Oxidation sollen die
Reaktionen 11-16 betrachtet werden. Während 11 als Ausgangsreaktion
geschwindigkeitsbestimmend ist, laufen die Reaktionen 12, 13 und 16 sehr
schnell ab. Sie verbrauchen dabei das CH2OH, CH2O und CHO
schneller als diese Komponenten jeweils gebildet werden und liefern damit die
kinetische Grundlage für die Stationaritätsannahmen
für diese Komponenten. Zusätzlich werden die Komponenten O und OH als stationär
angenommen, während das Radikal H weiterhin als nichtstationäre Komponente im
Mechanismus erhalten bleiben soll. Addiert man zu der Hauptkette nun die
Reaktion 3b, so ergibt die Addition
11 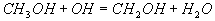
12 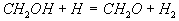
13 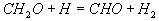
16 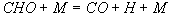
3b 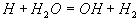
I 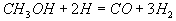
Diese Brutto-Reaktion I beschreibt somit die Teiloxidation
von CH3OH zu den nicht-stationären Komponenten CO und H2 . Eine Brutto-Reaktion für die Oxidation von CO
erhält man durch Addition von 9 und 3b
9 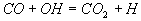
3b 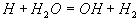
II 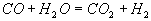
Dies ist die bekannte Wassergas-Reaktion. Der Einfluß der kettenabbrechenden Reaktion 5 wird deutlich,
wenn man die Reaktionen 5 und 7 addiert.
5 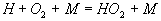
7 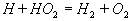
III 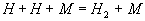
Schließlich erhält man eine in der Summe kettenverzweigende
Reaktion, wenn man zu Reaktion 1 die Reaktion 2 und zweimal die Reaktion 3f
addiert.
1 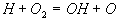
2 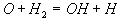
3f 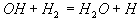
3f 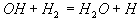
IV 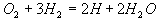
Daraus ergibt sich der Vier-Schritt-Mechanismus für die Methanolverbrennung (vergl.[ii][2])
Gleichungen 3.3-9:
I 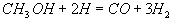
II 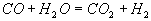
III 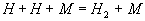
IV 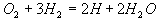
Ähnliche reduzierte Mechanismen sind auch für andere
Kohlenwasserstoffe hergeleitet und anhand laminarer Flammen getestet worden [iii][3].
In neuester Zeit sind auch kinetische Mechanismen für die Referenzkraftstoffe
n-Heptan- und iso-Oktan-Luft-Flammen zusammengestellt
und auf die wesentlichen Globalreaktionen reduziert worden [iv][4],[v][5].
Für iso-Oktan ergibt sich z.B. ein
6-Schritt-Mechanismus mit den Globalreaktionen
Gleichungen 3.3-10:
I 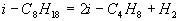
II 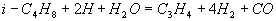
III 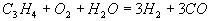
IV 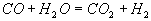
V 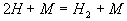
VI 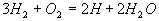
Aus derartigen reduzierten Mechanismen lassen sich
analytische Beziehungen zur Berechnung von Brenngeschwindigkeiten herleiten,
die jedoch algebraisch kompliziert sind. Darauf aufbauend wurden explizite
Approximationen von Brenngeschwindigkeiten für magere und stöchiometrische
Gemische von Methanol, iso-Oktan und n-Heptan mit
Luft über einem weiten Bereich von Drücken und Vorwärmtemperaturen entwickelt [vi][6]. In Abbildung 3.3-2 ist der Vergleich zwischen
numerisch berechneten und approximierten Brenngeschwindigkeiten sL für
stöchiometrische iso-Oktan-Luft Flammen als Funktion
des Druckes und der Temperatur Tu
des Gemisches angegeben. Es zeigt sich eine gegenläufige Tendenz, die dazu
führt, daß sich die Einflüsse der Temperaturerhöhung
und der Druckerhöhung aufgrund der Kompression des Gemisches weitgehend
kompensieren.

Abbildung 3.3-2: Laminare Brenngeschwindigkeiten von
iso-Oktan bei f=1.
Die Punkte stellen Berechnungen mit einem vollständigen kinetischen Mechanismus
dar, die durchgezogenen Linie die explizite Approximation.
3.3.2.5
Die Struktur laminarer Flammen
Eine Vormischflamme hat im Gegensatz zur Diffusionsflamme
die Fähigkeit, sich normal zu ihrer Oberfläche fortzubewegen. Diese
Fortbewegung geht zurück auf chemische, diffusive und konvektive Effekte, was
bei Betrachtung der inneren Struktur der Vormischflamme deutlich wird (Abbildung 3.3-3). Die Flamme setzt sich
zusammen aus einer Vorwärmzone, in der noch keine chemischen Reaktionen
ablaufen, einer dünnen Reaktionszone sowie einer Oxidationszone. In der dünnen
Reaktionszone findet der Umsatz des Brennstoffs zu CO und H2
(entsprechend der Bruttoreaktion I in den Gleichungen 3.3-9 oder I-II in den Gleichungen 3.3-10) statt. Danach findet in der
Oxidationszone der relativ langsame Ausbrand von CO
und H2 statt. Die Vorwärmzone zeichnet sich durch ein Gleichgewicht
der konvektiven und diffusiven Prozesse aus, während in der Reaktionszone
chemische Reaktion und Diffusion im Gleichgewicht stehen. Diese Grundstruktur
ist für alle Kohlenwasserstoff- und Alkohol-Flammen gültig, wobei für
verschiedene Brennstoffe und Mischungsverhältnisse unterschiedliche Verläufe
von Temperatur- und Konzentrationsverläufen gefunden werden. Im stationären
Fall stellt sich die laminare Brenngeschwindigkeit als diejenige Geschwindigkeit
ein, mit der sich das unverbrannte Gemisch auf die Reaktionszone zubewegt. Es läßt sich eine globale chemische Zeit definieren, die die
gesamte chemische Reaktion charakterisiert. Die chemische Zeit und die laminare
Brenngeschwindigkeit sind miteinander gekoppelt aufgrund des
Wärmeleitungsprozesses in der Vorwärmzone. Es läßt
sich somit dimensionsanalytisch eine laminare Brenngeschwindigkeit angeben
Gleichung 3.3-11: 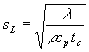
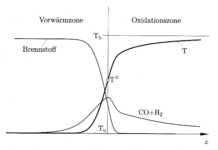
Abbildung 3.3-3: Konzentrations- und
Temperaturprofile in der Reaktionszone
Im Hinblick auf die Definition der laminaren Flammendicke
werden die stark temperaturabhängigen Stoffwerte l/cp
bei der Temperatur T0 und
die Dichte r bei der Temperatur des Unverbrannten Tu bestimmt. Die Referenztempertaur
T0 stellt die Temperatur
in der dünnen Reaktionszone dar (vergl. Abbildung 3.3-3). Bei der Annahme einer
chemisch inerten Vorwärmzone wird davon ausgegangen, daß
erst nach Erreichen dieser Temperatur Reaktionen einsetzen. Es kann dann
folgende Definition für die laminare Flammendicke angegeben werden
Gleichung 3.3-12: 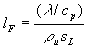
Diese Definition bezieht sich auf die Dicke der Vorwärmzone.
Die korrespondierende Flammenzeit tF=lF/sL
entspricht der bereits eingeführten chemischen Zeit tc.
3.3.3 Turbulente
Flammenausbreitung
Die Ausbreitung einer Flammenfront in einem turbulenten
homogenen Kraftstoff-Luft-Gemisch wird durch zwei wesentliche Mechanismen beeinflußt: Die Reaktionskinetik und die daraus
resultierende laminare Brenngeschwindigkeit und die turbulente
Strömungsbewegung, die durch die Turbulenzintensität charakterisiert wird. Ein
zentraler Parameter der turbulenten vorgemischten Verbrennung ist daher die
Relation zwischen diesen beiden Effekten, welche durch das
Geschwindigkeitsverhältnis v'/sL wiedergegeben wird. Die Fähigkeit des
turbulenten Strömungsfeldes, die turbulente Flammenausbreitung zu beeinflussen,
wird darüberhinaus durch das Verhältnis
charakteristischer Längenskalen von Strömungsfeld und laminarer Flamme
beschrieben werden, welche im folgenden
detailliert vorgestellt werden.
3.3.3.1
Längenskalen des turbulenten Strömungsfeldes
Die turbulente Strömungsbewegung, die zunächst als ein
chaotischer Vorgang betrachtet werden kann, muß zur
Quantifizierung ihrer Eigenschaften mit geeigneten statistischen Verfahren
beschrieben werden. Die einfachste Form einer solchen Beschreibung ist die
bereits von Reynolds eingeführte Aufteilung der lokalen
Strömungsgeschwindigkeit u in einen
mittleren Anteil 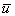 und eine überlagerte Schwankungsbewegung u'
und eine überlagerte Schwankungsbewegung u'
Gleichung 3.3-13: 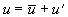
Diese Betrachtung bezieht sich auf den örtlichen Vorgang und
enthält keinerlei Aussagen über räumliche Strukturen des turbulenten
Strömungsfeldes. Sie ist jedoch gut geeignet, um Messungen zu interpretieren,
die bisher überwiegend als zeitlich aufgelöste Punktmessungen möglich waren
(LDA, Hitzdraht-Anemometrie). In diesem Abschnitt
soll auch über PIV-Messungen berichtet werden, die im Teilprojekt A2
durchgeführt wurden.
Die Varianz der Geschwindigkeit 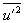 beschreibt die Geschwindigkeitsfluktuationen.
Als Turbulentintensität v’ wird die Wurzel aus den algebraischen Mitteln der Varianzen der
drei Geschwindigkeitskomponenten u , v und w bezeichnet
beschreibt die Geschwindigkeitsfluktuationen.
Als Turbulentintensität v’ wird die Wurzel aus den algebraischen Mitteln der Varianzen der
drei Geschwindigkeitskomponenten u , v und w bezeichnet
Gleichung 3.3-14: 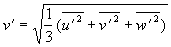
Im Falle einer als isotrop angenommenen Turbulenz (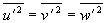 )
ist daher die Turbulenzintensität
)
ist daher die Turbulenzintensität
Gleichung 3.3-15: 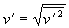
Für jede einzelne Komponente wird die Wurzel aus der Varianz
im folgenden als RMS (root mean
square) bezeichnet.
Die Turbulenzintensität enthält somit keine Aussage über die
Frequenz dieser Schwankungen. Trotz dieser statistisch grob vereinfachten
Darstellung der Turbulenz konnten erfolgreiche Modelle entwickelt werden,
welche die durch die Turbulenz scheinbar veränderten Transportgrößen
(turbulente Scheinzähigkeit) abschätzen und die Berechnung turbulenter
Strömungen ermöglichen. Eine deutliche Verbesserung dieser
Turbulenzbeschreibung wurde durch die Hypothesen von A.N. Kolmogorov erreicht.
Sie basieren auf der Grundvorstellung, daß eine
turbulente Strömung Einzelwirbel verschiedener Größe enthält, die miteinander
in Interaktion treten und kinetische Energie austauschen. Die Turbulenzenergie
wird durch Gradienten des mittleren Strömungsfeldes in Form großer Wirbel
produziert und in einer Energiekaskade auf Wirbel kleinerer Größe übertragen,
bis schließlich die viskose Dissipation erfolgt. Die charakteristischen
Längenmaße des turbulenten Strömungsfeldes beschreiben die Größenordnungen,
zwischen denen diese Austauschprozesse ablaufen. Die Abmessung der
energiereichsten turbulenten Wirbelelemente wird durch das integrale Längenmaß lt
beschrieben. Dieses Längenmaß ist in starkem Maße von der Geometrie der
betrachteten Strömung abhängig und wird z.B. in einer Freistrahlströmung als
proportional zur Freistrahlbreite angenommen. Für die Strömung in motorischen
Brennräumen hat sich als Abschätzung des integralen Längenmaßes in der Nähe des
oberen Totpunktes 10-20 % des Abstandes zwischen Kolbenboden und Zylinderkopf
als realistisch erwiesen. Das integrale Längenmaß stellt die energiereichsten
turbulenten Strukturen dar. Es ist jedoch kleiner als die makroskopischen
Strukturen des Strömungsfeldes (z.B. Drall- oder Tumble-Wirbel
im Brennraum), die durch die Einlaufströmung entstehen. Eine Bestimmung des
integralen Längenmaßes ist möglich durch Messung der Geschwindigkeit an zwei
Punkten im Abstand r und durch
Auswertung der räumlichen Zweipunktkorrelation
Gleichung 3.3-16: 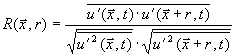 ,
,
wobei das Längenmaß definiert ist zu
Gleichung 3.3-17: 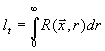 .
.
Diese Definition des integralen Längenmaßes basiert auf der
anschaulichen Überlegung, daß für
Korrelationsabstände r<lt eine Ähnlichkeit des
Geschwindigkeitsverlaufes an zwei Punkten vorliegt, während diese Ähnlichkeit
für r>lt
verloren geht. Das integrale Längenmaß stellt die obere Grenze des Inertialbereiches dar, in welchem die turbulente kinetische
Energie in Form einer Kaskade von den großen zu kleineren Wirbelelementen
übertragen wird. Aus der Annahme der Lokalität der Energieübertragung
(Übertragung nur auf das nächst kleinere Wirbelelement) folgt die Unabhängigkeit
der Energietransferrate (Energieübertragung pro Zeiteinheit) von der
Wirbelgröße ln . Innerhalb
der Energiekaskade ist die Energietransferrate konstant und wird schließlich
bei dem kleinsten Wirbelelement, dem Kolmogorov-Wirbel, gleich der Dissipation 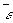 .
Ein Wirbelelement der Größe ln mit der assoziierten
Geschwindigkeitsschwankung
.
Ein Wirbelelement der Größe ln mit der assoziierten
Geschwindigkeitsschwankung 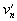 hat die kinetische Energie
hat die kinetische Energie 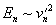 und eine charakteristische Umdrehungszeit
und eine charakteristische Umdrehungszeit 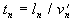 .
Die Energietransferrate = Dissipation ist dann unabhängig von n und wird aus Dimensionsgründen
.
Die Energietransferrate = Dissipation ist dann unabhängig von n und wird aus Dimensionsgründen
Gleichung 3.3-18: 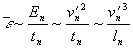
Daraus ergeben sich die folgenden Abschätzungen für die
kinetische Energie, die Umdrehungsgeschwindigkeit und die Umdrehungszeit eines
Wirbels der Größe ln
Gleichung 3.3-19: 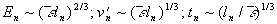
Das integrale Längenmaß sowie das korrespondierende
integrale Zeitmaß kann auch durch Dimensionsanalyse werden zu
Gleichung 3.3-20: 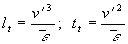
Um die Verteilung der Turbulenzenergie auf die verschiedenen
Wirbelgrößen zu erhalten, wird die Energie einer diskreten Wirbelgröße durch
die spektrale Energiedichte E(k)
ausgedrückt
Gleichung 3.3-21: 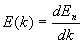
Dabei ist 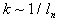 die Wellenzahl. Mit Gleichung 3.3-19 ergibt sich
die Wellenzahl. Mit Gleichung 3.3-19 ergibt sich
Gleichung 3.3-22: 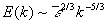
Dies ist die charakteristische spektrale Verteilung der
Turbulenzenergie im Inertialbereich. Die obere Grenze
des Inertialbereiches im Wellenzahlraum wird durch
die Kolmogorov-Länge bestimmt - die kleinstmögliche Wirbelgröße bei welcher die
kinetische Energie durch viskose Dissipation in Wärme übergeht. Da diese
kleinste Wirbelgröße von der Viskosität des Fluids sowie von der Dissipationsrate
abhängen muß, ergibt sich aus Dimensionsgründen für
das Längenmaß und die zugehörigen Zeit- und Geschwindigkeitsmaße
Gleichung 3.3-23: 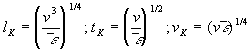
Ein weiteres Längenmaß, die Taylorlänge
Gleichung 3.3-24: 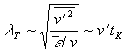 ,
,
charakterisiert den mittleren Gradienten des
Geschwindigkeitsfeldes und liegt zwischen integralem Längenmaß und der
Kolmogorov Länge. Die Taylor-Länge kann als Distanz angesehen werden, um welche
ein Kolmogorov-Wirbel während seiner Umdrehungszeit tk durch die größten
turbulenten Wirbel transportiert wird.
3.3.3.2
Messung der Spektralen Energiedichte im Einhubtriebwerk
Innerhalb des Teilprojektes A5 wurde ein Einhubtriebwerk
(s. Abbildung
3.3-4)
entwickelt, das es ermöglicht, eine quasi zweidimensionale turbulente Flamme
unter motorischen Bedingungen zu realisieren und ihre Entwicklung zu beobachten
und zu untersuchen [vii][7],[viii][8],[ix][9],[x][10]. Die ebene Flammengeometrie
gestattet bei optischen Untersuchungen Frischgas, Flammenzone und Abgas zu
unterscheiden, wobei die Struktur der Flammenzone mit quantitativen Aufnahmen
der Eigenstrahlung in ihrer örtlichen und zeitlichen Entwicklung untersucht
werden kann.
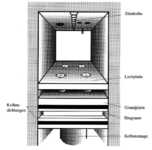
Abbildung 3.3-4: Darstellung des Brennraumes des Einhubtriebwerkes
In den Kolben des Einhubtriebwerks
ist ein Turbulenzgenerator integriert, bestehend aus einer Lochplatte, welche
durch den Brennraum gezogen wird. Die von den Löchern hervorgerufenen
Freistrahlen sind den Einlaßstrahlen beim Ottomotor
ähnlich. Aus diesem Grunde sind die Ergebnisse, welche aus den LDA-Messungen
erhalten wurden, auf zyklisch arbeitende Motoren übertragbar, da auch der
Kompressionshub im Einhubtriebwerk nachgebildet
wurde.

Abbildung 3.3-5: Spektrale Energieverteilung,
Abklingzeit der Turbulenz tA=6 ms, ohne
Kompression
Für drei verschiedene Turbulenzgeneratoren wurden die
spektralen Energiedichten Eu und Ev in axialer und in radialer Richtung ermittelt.
Ohne Kompressionseinfluß erkennt man bei Versuchen
mit 4-Loch-Platte in Abbildung
3.3-5
unabhängig von der Kolbenverzugszeit im Frequenzbereich oberhalb von 200 Hz
eine sehr gute Übereinstimmung mit der für isotrope Turbulenz geltenden
Steigung von -5/3 (vergl. Gleichung
3.3-22).
Die teilweise starke Abweichung der Verläufe für beide
Geschwindigkeitskomponenten im Frequenzbereich unter 200 Hz wird durch
niederfrequente Gasbewegungen hervorgerufen. Kurz nach Ende der
Turbulenzproduktion existieren noch durch die Freistrahlen hervorgerufene
grobballige Strukturen im Strömungsfeld, die sich im Verlauf des
Abklingvorganges auflösen.
3.3.3.3
Messung der Turbulenzintensitäten und der turbulenten Längenmaße im
geschleppten Motor
In den Teilprojekten A2 und A7 wurden Turbulenzmessungen
während des Kompressionshubs im geschleppten Motor durchgeführt. Dabei wurde im
Teilprojekt A7 mit einem 2-Punkt LDA-Verfahren und im Teilprojekt A2 mit dem
PIV-Verfahren gearbeitet. In Abbildung 3.3-6 ist der Intensitätsverlauf
der Geschwindigkeitsschwankungen (RMS-Wert) über dem Grad Kurbelwinkel für die
radiale und die axiale Schwankungsgröße dargestellt. Der RMS-Wert, der mit der
axialen Richtung der Geschwindigkeitskomponente gebildet wird, verläuft auf
einem niedrigeren Niveau als der RMS-Wert, der mit der radialen
Geschwindigkeitskomponente gebildet wird. Beide Verläufe sind aber von der
gleichen Größenordnung. Gegen Ende der Kompression ist für den axialen Verlauf
ein leichtes Ansteigen festzustellen, während für den radialen Verlauf ein
leichtes Abfallen auftritt. Vergleicht man diese Ergebnisse mit den aus
LDA-Messungen ermittelten RMS-Werten, die im Teilprojekt A7 durchgeführt wurden [xi][11],[xii][12], so sind die hier erzielten Werte von
der gleichen Größenordnung.
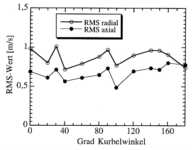
Abbildung 3.3-6: RMS-Wert
während der Kompression
Es sind zwei
integrale Längenmaße gemessen worden, die aus einer Korrelation der axialen
Schwankungsgeschwindigkeit in axialer Richtung und aus einer Korrelation der
radialen Schwankungsgeschwindigkeit in radialer Richtung gebildet wurden. Beide
Verläufe sind in Abbildung 3.3-7 dargestellt. Das integrale Längenmaß in
radialer Richtung verläuft auf einem höheren Niveau als dasjenige in axialer
Richtung. Zum Ende des Kompressionstaktes ist eine Abnahme des radialen
Längenmaßes und eine Zunahme des axialen Längenmaßes festzustellen. Insofern
nähert sich die Turbulenz zum Ende des Kompressionstaktes dem isotropen
Zustand. Die hier gefundenen Längenmaße stimmen in der Größenordnung mit denen,
die im Teilprojekt A7 durch LDA-Messungen ermittelt wurden [xiii][11],[xiv][12] überein.
Das Anwachsen des integralen axialen Längenmaßes bei der Annäherung an den
oberen Totpunkt widerspricht der Vorstellung, die von der axialen Kompression
eines ursprünglich kugelförmigen turbulenten Elementes ausgeht. Es handelt sich
bei dem integralen Längenmaß nicht um eine physikalische Abmessung, die durch
Kompression gestaucht werden könnte, sondern entsprechend Gleichung 3.3-17 um eine Korrelationslänge.
Durch axiale Kompression wird die Korrelation innerhalb des Strömungsfeldes in
axialer Richtung erhöht, und daher erhöht sich auch das integrale Längenmaß in
axialer Richtung. Ein derartiges Verhalten ist in [xv][13]
vorhergesagt worden.
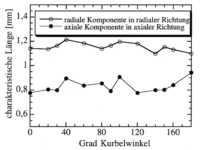
Abbildung 3.3-7: Integrales Längenmaß während der
Kompression
In Abbildung
3.3-8
ist das integrale Längenmaß, das Taylorsche
Mikrolängenmaß und die Kolmogorov-Länge aufgetragen. Zu Beginn der Kompression
unterscheiden sich integrale Länge und Kolmogorov-Länge um mehr als eine
Größenordnung. Während der Kompression ändert sich das integrale Längenmaß
nicht, während die beiden anderen Längen abfallen. Die Kolmogorov-Länge wird
dabei um eine Größenordnung kleiner und hat im oberen Totpunkt eine Länge in
der Größenordnung von 0.01 mm. Da im oberen Totpunkt die Entflammung und
Flammenausbreitung eines Brennstoff-Luft Gemisches stattfindet, kann man die
hier gefundenen Längen der Strömungsturbulenz mit den weiter unten
präsentierten Längen der Flammenfront vergleichen.
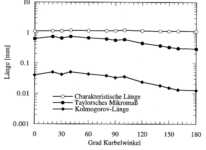
Abbildung 3.3-8: Turbulente Längenmaße während der
Kompression eines geschleppten Ottomotors
3.3.3.4
Längenskalen der Interaktion von Turbulenz und Flammenausbreitung
Nach der Definition der charakteristischen Längenskalen von
turbulentem Strömungsfeld und laminarer Flammenstruktur können nun weitere
Längenskalen angegeben werden, welche die Interaktion beider Vorgänge
charakterisieren. Zunächst können zwei Längenmaße der Flammenstruktur definiert
werden, die in Analogie zu den charakteristischen Längenmaßen des turbulenten
Strömungsfeldes stehen. Die Größenordnung der größten turbulenten
Flammenstrukturen wie sie z.B. in Abbildung 3.3-1 sichtbar werden, sind auf die
Interaktion der Flammenfront mit den großen turbulenten Wirbelelementen des
Strömungsfeldes zurückzuführen. Als ein weiteres, die großen turbulenten
Strukturen charakterisierendes Längenmaß ist die turbulente Flammendicke lF,t zu nennen, für welche eine Proportionalität
zum integralen Längenmaß der Flammenstruktur erwartet werden kann. Die
Bezeichnung Flammendicke deutet bereits darauf hin, daß
dieses Längenmaß als die Dicke oder Breite der Fluktuationszone bezeichnet
werden kann, in der sich eine ebene turbulente Vormischflamme relativ zu ihrer
mittleren Position bewegt.
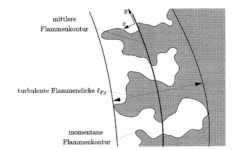
Abbildung 3.3-9: Die turbulente Flammendicke und die
Taylor-Länge der Flammenstruktur
Definiert werden kann die turbulente Flammendicke als die
doppelte Varianz der Aufenthaltswahrscheinlichkeit der Flamme, bezogen auf die
mittlere Position
Gleichung 3.3-25: 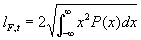
Sie ist in Abbildung 3.3-9 schematisch dargestellt. Die
Betrachtung der kinematischen Interaktion von laminarer Flammenfront und
turbulenter Strömung führt auf ein wesentliches Längenmaß, die Gibson-Länge lG [xvi][14]. Ausgangspunkt ist erneut die
Annahme des turbulenten Strömungsfeldes als ein Ensemble diskreter Wirbel
verschiedener Größen ln . Die
Umfangsgeschwindigkeit dieser Wirbel ergibt sich entsprechend Gleichung 3.3-19 zu
Gleichung 3.3-26: 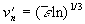 ,
,
wenn man der Einfachheit halber das
Gleichheitszeichen verwendet.
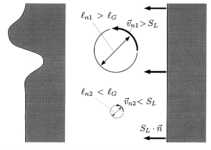
Abbildung 3.3-10: Interaktion einer laminaren
Flammenfront mit diskreten Wirbeln verschiedener Größenordnungen
Wie in Abbildung
3.3-10
dargestellt, können nur Wirbel der Flammenfront eine Struktur aufprägen und
damit die Flammenfront auffalten, deren Umfangsgeschwindigkeit größer ist als
die laminare Brenngeschwindigkeit der Flammenfront. Kleinere Wirbel mit
entsprechend geringerer Umfangsgeschwindigkeit werden von der Flammenfront
überlaufen, ohne signifikante Strukturen erzeugen zu können. Die Größenordnung
der kleinsten Wirbel, die in der Lage sind, die Flammenfront zu beeinflussen,
wird durch die Gibsonlänge lG
dargestellt. Aus 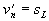 ergibt sich
ergibt sich
Gleichung 3.3-27: 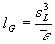 .
.
Mit Gleichung
3.3-20
kann das Längenskalenverhältnis gebildet werden
Gleichung 3.3-28: 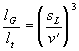 .
.
Das integrale Längenmaß kann im Falle der motorischen
Verbrennung als konstant angesehen werden. Somit ergibt sich folgende
Abhängigkeit der Gibsonlänge vom Verhältnis v'/sL
Gleichung 3.3-29: 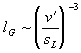 .
.
Es sind also bei steigender Turbulenzintensität im
Motorbrennraum zunehmend kleinere Strukturen zu erwarten, die zu einer
Vergrößerung der turbulenten Flammenoberfläche beitragen können.
Um eine möglichst genaue Beschreibung der Interaktion des
turbulenten Strömungsfeldes mit der laminaren Flammenausbreitung zu erhalten,
ist ein weiteres charakteristisches Längenmaß von Interesse, welches die
lokalen Einflüsse des Strömungsfeldes auf die Flammenstruktur quantifiziert.
Diese führen zu einer lokalen Abweichung der laminaren Brenngeschwindigkeit von
ihrem Referenzwert 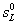 einer ebenen Vormischflamme in ruhendem
Gemisch. Verantwortlich für diese lokale Abweichung ist die Streckung der
Flammenstruktur, welche durch Flammenfrontkrümmung und lokale Divergenz des
Strömungsfeldes hervorgerufen wird.
einer ebenen Vormischflamme in ruhendem
Gemisch. Verantwortlich für diese lokale Abweichung ist die Streckung der
Flammenstruktur, welche durch Flammenfrontkrümmung und lokale Divergenz des
Strömungsfeldes hervorgerufen wird.
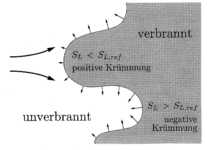
Abbildung 3.3-11: Lokaler Einfluß
des Strömungsfeldes auf die laminare Brenngeschwindigkeit
Als „Proportionalitätsfaktor“, der das Maß dieser
Abhängigkeit skaliert, wird die Marksteinlänge L eingeführt [xvii][15].
Die Marksteinlänge ist von der Größenordnung der laminaren Flammendicke lF ,
das Verhältnis L/lF wird als Marksteinzahl
M bezeichnet. Streckung und Krümmung können die lokalen Bedingungen von
Diffusion und Wärmeleitung stark beeinflussen, was zur Änderung der lokalen
laminaren Brenngeschwindigkeit führt. Die lokale laminare Brenngeschwindigkeit
unter dem Einfluß von Krümmung k und Streckung  konnte in
9 angegeben werden zu
konnte in
9 angegeben werden zu
Gleichung 3.3-30: 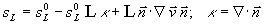 .
.
Die lokale Krümmung k
der Flammenfront ist entsprechend Abbildung 3.3-11 positiv definiert für
Bereiche, die konvex zum unverbrannten Gemisch gewölbt sind. Dies folgt
ebenfalls aus der Definition von k in
Gleichung
3.3-30,
da der Normalenvektor auf der Flammenfront zum Unverbrannten orientiert ist.
Ein Vergleich zwischen berechneten und gemessenen Markstein-Zahlen für Propan
zeigt Abbildung
3.3-12.
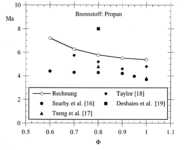
Abbildung 3.3-12: Vergleich der berechneten und der
experimentellen Markstein Zahlen für Propan bei p=1bar und einer Vorwärmtemperatur von 298K (aus [xviii][6])
3.3.3.5
Messung der Interaktionslängen bei der turbulenten Flammenausbreitung
In Teilprojekt A2 sind die verschiedenen Längenmaße, die
sich aus der Interaktion von Turbulenz und Verbrennung ergeben, in dem
Transparentmotor der in Abschnitt 3.3.1 bereits beschrieben wurde,
gemessen worden [xix][16].
Als Kraftstoff wurde Propan verwendet um eine möglichst homogene Mischung zu
erzielen. Dem Kraftstoff-Luft-Gemisch wurden Rauchpartikel beigegeben, die in der
Flammenfront verbrennen. Durch einen Laser-Lichtschnitt, in dem nur die
Rauchpartikel und damit der unverbrannte Bereich sichtbar wird, kann die
momentane Flammenkontur ermittelt werden.
Als Laserquelle wurde ein Nd:YAG-Laser eingesetzt. Die Belichtungszeit der
Flammenfrontaufnahmen liegt bei ca. 8 ns und somit um
mehrere Größenordnungen unterhalb aller für die Flammenausbreitung
charakteristischen Zeitskalen. Mit einer maximalen Pulswiederholrate des Lasers
von 40 Hz kann pro Motorzyklus eine Lichtschnitt-Aufnahme aufgezeichnet werden.
Abbildung
3.3-13
zeigt schematisch die optische Anordnung zur Bildaufzeichnung
im VW-Transparentmotor. Eine wichtige Voraussetzung für örtlich hochaufgelöste
Lichtschnittaufnahmen ist die Lichtschnittdicke. Da die Flammenfront in der
Regel nicht überall senkrecht zur Lichtschnittebene steht, stellt die
Lichtschnittdicke die untere Grenze der auflösbaren Strukturen dar, was im Fall
der motorischen Verbrennung von besonderer Bedeutung ist.
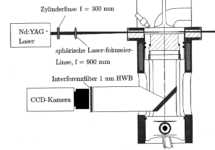
Abbildung 3.3-13:
Optischer Aufbau für Laser-Lichtschnittaufnahmen am VW-Transparentmotor
In Abbildung
3.3-14
ist die Anordnung des abgebildeten Bereiches im Motorbrennraum dargestellt. Die
Wahl des abgebildeten Bereiches erfolgte nach der Maßgabe, daß
die kleinste auflösbare Längenskala, die der Lichtschnittdicke entspricht, von
der Auflösung der verwendeten Kamera eindeutig überschritten wird. Diese
Bedingung ist durch die Verwendung einer CCD-Kamera mit einer Auflösung von
581x756 Pixeln erfüllt. Es konnte demnach die gesamte Breite des im VW-Motor
realisierbaren Lichtschnittes erfaßt werden. Ferner
war bei diesem Vergrößerungsverhältnis die Erfassung der kleinsten
charakteristischen Längenskalen, der Gibson-Länge lG , und der
größten charakteristischen Längenskalen, der turbulenten Flammendicke lF,t, in einer Aufnahme
möglich.
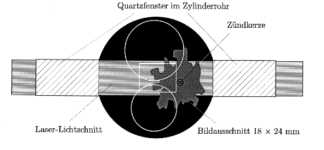
Abbildung 3.3-14: Anordnung von Laser-Lichtschnitt und
Bildbereich im Brennraum des VW-Transparentmotors
In Abbildung 3.3-14: Anordnung von Laser-Lichtschnitt und
Bildbereich im Brennraum des VW-Transparentmotors
ist eine bereits mit
einem Bildverarbeitungssystem gefilterte Aufnahme der momentanen Flammenkontur
dargestellt. Die Flammenkontur wird dabei digitalisiert und kann sodann einer
mathematischen Analyse unterworfen werden [xx][17]. Es wurde sowohl eine Analyse
auf der Basis der Theorie der Fraktale als auch eine spektrale Auswertung
durchgeführt. Die spektrale Analyse, die durch eine theoretische Formulierung
mittels Zweipunktkorrelation ergänzt wird [xxi][18], führt
mittels einer Fourier-Transformation der Flammenkontur zu einer spektralen
Schwankungsdichte G(k) der
Flammenfrontstrukturen, die in Analogie zur spektralen Energiedichte der
Turbulenzenergie (Gleichung
3.3-22
und Abbildung
3.3-5)
steht. Es ergibt sich eine theoretische Vorhersage der Form

Abbildung 3.3-15: Turbulente Flammenfront bei der
Flammenausbreitung im Ottomotor
Gleichung 3.3-31: 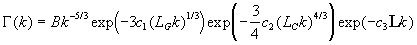 .
.
Dabei ist LC
die Corrsin-Länge, die als Funktion der Gibson-Länge
und der Markstein-Länge ausgedrückt werden kann
Gleichung 3.3-32: 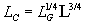
Die Parameter B, c1,
c2 und c3
sind noch unbekannte Modellierunskonstanten, die
durch Anpassung an gemessene spektrale Schwankungsdichten ermittelt werden
können. Hier wurde c1 =1, c2 =2 und c3 =1 gesetzt und das
theoretische Spektrum mit den Meßwerten so zur
Deckung gebracht, daß die Gibson-Länge berechnet
werden kann. Abbildung
3.3-16
zeigt eine sehr gute Übereinstimmung zwischen den Meßwerten
der spektralen Schwankungsdichte und der angepaßten
Spektralfunktion nach Gleichung
3.3-31.
Beide unterscheiden sich deutlich von dem Grenzverhalten für kleine
Wellenzahlen, das wie die spektrale Energiedichte nach einem -5/3 Gesetz
verläuft. Der Übergang bei der Gibson-Länge LG
ist nicht so abrupt wie es für das Energiespektrum erwartet wird. Dort würde
eine ähnliche Form wie Gleichung
3.3-31
gelten, jedoch die erste und letzte Exponentialfunktion würde entfallen und
statt der Corrsin-Länge die Kolmogorov-Länge
einzusetzen sein. Hier übernimmt die Gibson-Länge die Funktion der
Kolmogorov-Länge. Sie stellt somit die kleinste charakteristische Länge in der
Flammenkontur dar.
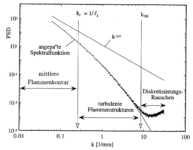
Abbildung 3.3-16: Spektrale Schwankungsdichte der räumlichen
Flammenstrukturen
Die verschiedenen charakteristischen Längen der
Flammenkontur sind in Abbildung
3.3-16
zusammenfassend als Funktion von v'/sL dargestellt. Diese Variation von v'/sL
entspricht einer Variation der Motordrehzahl von 500 bis 2500 Umdrehungen pro
Minute. Es wurden Messungen für l=1.0
und l=1.6 mit Propan als Kraftstoff durchgeführt.
Die Turbulenzintensität v' wurde zu
0.5 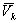 gesetzt, wobei
gesetzt, wobei 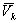 die mittlere Kolbengeschwindigkeit ist. Die so
ermittelten Werte von v'/sL sind in Abbildung 3.3-17 dargestellt. Abbildung 3.3-16 ist gemeinsam mit Abbildung 3.3-8 zu betrachten. Dabei zeigt
sich, daß die verschiedenen turbulenten Längenmaße
des Strömungsfeldes deutlich voneinander getrennt sind. Das integrale Längenmaß
ist im oberen Totpunkt um zwei Größenordnungen größer als die Kolmogorov-Länge,
die wiederum von der Größenordnung der laminaren Flammendicke ist. Dazwischen
liegt die Taylor-Länge, die turbulente Flammendicke, die Gibson-Länge und die
Markstein-Länge. Diese Trennung der Längenmaße zeigt eindeutig, daß die Verbrennung im Otto-Motor in diesem Drehzahl-Bereich
im Flamelet-Regime angesiedelt ist (vergl. Abbildung 3.3-19).
die mittlere Kolbengeschwindigkeit ist. Die so
ermittelten Werte von v'/sL sind in Abbildung 3.3-17 dargestellt. Abbildung 3.3-16 ist gemeinsam mit Abbildung 3.3-8 zu betrachten. Dabei zeigt
sich, daß die verschiedenen turbulenten Längenmaße
des Strömungsfeldes deutlich voneinander getrennt sind. Das integrale Längenmaß
ist im oberen Totpunkt um zwei Größenordnungen größer als die Kolmogorov-Länge,
die wiederum von der Größenordnung der laminaren Flammendicke ist. Dazwischen
liegt die Taylor-Länge, die turbulente Flammendicke, die Gibson-Länge und die
Markstein-Länge. Diese Trennung der Längenmaße zeigt eindeutig, daß die Verbrennung im Otto-Motor in diesem Drehzahl-Bereich
im Flamelet-Regime angesiedelt ist (vergl. Abbildung 3.3-19).
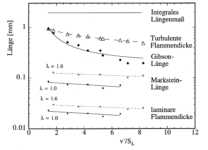
Abbildung 3.3-17: Charakteristische Längenskalen der
turbulenten Flammenausbreitung im Ottomotor
17
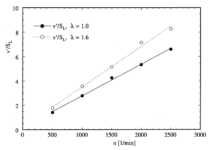
Abbildung 3.3-18: Die Werte von v'/sL für die verschiedenen
Betriebspunkte
3.3.3.6
Regimes der turbulenten vorgemischten Verbrennung
Nach Einführung der charakteristischen Längenskalen von
Strömungsfeld, Flammenstruktur und Interaktion beider Prozesse kann nun eine
Einteilung der vorgemischten Flammenausbreitung in verschiedene Regimes
erfolgen, die mit jeweils unterschiedlichen Modellen zu beschreiben sind [xxii][14],[xxiii][19].
Hierzu werden zunächst drei Kennzahlen bereitgestellt.
Eine turbulente Reynoldszahl kann mit der Referenzviskosität
nref=sL lF gebildet werden
Gleichung 3.3-33: 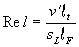 .
.
Die turbulente Damköhlerzahl
Gleichung 3.3-34: 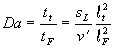
beschreibt das Verhältnis zwischen turbulenter Zeit und
Flammenzeit. Die turbulente Karlovitz-Zahl
Gleichung 3.3-35: 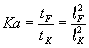
das Verhältnis von Flammenzeit zu Kolmogorov-Zeitmaß. In
einem von Borghi vorgeschlagenen Phasendiagramm der vorgemischten turbulenten
Verbrennung (Abbildung
3.3-19)
werden durch die Beziehung
Gleichung 3.3-36: 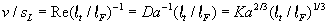
die Grenzen der verschiedenen Regimes definiert.
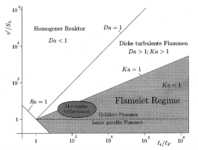
Abbildung 3.3-19: Phasendiagramm der vorgemischten
turbulenten Verbrennung
Neben den Regimes der laminaren Flammen (Re < 1) und des homogenen Reaktors (Da < 1, Chemie ist langsam im
Vergleich zur Turbulenz) ist für die Betrachtung der motorischen Verbrennung
vor allem das Flamelet-Regime und bedingt das Regime
der dicken turbulenten Flammen von Bedeutung. Im unteren Bereich des Flamelet-Regimes, den leicht gewellten Flammen mit v'/sL
< 1 , dominiert die laminare Flammenausbreitung -
selbst die größten Wirbel können die Flamme nicht signifikant beeinflussen. Der
für die motorische Verbrennung in erster Linie relevante Bereich der gefalteten
Flammen ist gekennzeichnet durch die Bedingungen stärkerer Turbulenz (Re > 1), gegenüber den turbulenten
Zeitskalen schneller Chemie (Da >
1), aber noch nicht zu starker lokaler Streckung (Ka < 1). Die laminare Flammendicke ist in diesem Regime kleiner
als alle turbulenten Längenmaße - die Flamme kann als dünn gegenüber den
turbulenten Strukturen des Strömungsfeldes angesehen werden. Erst wenn oberhalb
der Grenze (Ka = 1) die Flammendicke lF die
Kolmogorov-Länge übersteigt, treten örtliche Löscherscheinungen auf und es kann
nicht mehr von einer einfach zusammenhängenden Flammenoberfläche gesprochen
werden, da die kleinsten Wirbelelemente der Strömung durch ihre starke lokale
Streckung das Verlöschen und somit eine lokale Homogenisierung der
Reaktionszone herbeiführen. Steigt die Turbulenz so stark an, daß selbst die größten Wirbelelemente dazu in der Lage sind
(Da < 1), ist das Regime des
homogenen Reaktors erreicht - durch turbulente Mischung finden im gesamten Feld
Reaktionen statt.
Die für die ottomotorische
Verbrennung relevanten Bereiche dieses Phasendiagramms lassen sich anhand der
zu erwartenden Werte von v'/sL und lt / lF lokalisieren (Abbildung 3.3-19). Während sich die
Flammenausbreitung bei stöchiometrischem Luftverhältnis aufgrund der
Druckabhängigkeit der laminaren Flammendicke selbst bei hoher Last und Drehzahl
im Flamelet-Regime bewegt, kann insbesondere bei
magerem Luftverhältnis sowie bei hoher Drehzahl und niedriger Last das Regime
der dicken turbulenten Flammen erreicht werden.
3.3.3.7
Modelle zur Beschreibung der turbulenten Flammenausbreitung in vorgemischten
Systemen
Die Geschwindigkeit des Umsatzes der motorischen Verbrennung
wird bestimmt durch die laminare Brenngeschwindigkeit sL sowie die momentane
Flammenoberfläche F. Die für die
laminare Brenngeschwindigkeit relevanten Größen (Luftverhältnis und
thermodynamischer Zustand des Gemisches) sind nicht von der Motordrehzahl
abhängig. Die mit der Drehzahl ansteigende Umsatzgeschwindigkeit kann somit nur
durch eine Vergrößerung der Flammenoberfläche durch turbulente Auffaltung
erklärt werden (Abbildung
3.3-20).
Für numerische Simulationen eignet sich besonders die
Zusammenfassung aller den Verbrennungsumsatz steigernden Effekte zu einer
turbulenten Brenngeschwindigkeit sT, der Geschwindigkeit, mit der sich eine ebene
turbulente Vormischflamme fortbewegt. Sie entspricht im stationären Fall der
mittleren Geschwindigkeit, mit der das Gemisch in die Flammenzone eintritt.
Gelingt es, diese turbulente Brenngeschwindigkeit in ihrer Abhängigkeit von
allen relevanten Einflußgrößen zu beschreiben, so
kann die Flammenausbreitung mit vergleichsweise einfachen Modellen beschrieben
werden, die z.B. eine kugelförmige Ausbreitung der Flammenfront um die
Zündkerze annehmen. Einer genauen Beschreibung der turbulenten
Brenngeschwindigkeit kommt daher für derartige Modelle zentrale Bedeutung zu.
Damköhler stellte schon 1940 mit Hilfe einer Analogie zur Bunsenflamme folgenden linearen Zusammenhang auf
Gleichung 3.3-37: 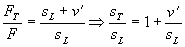 .
.
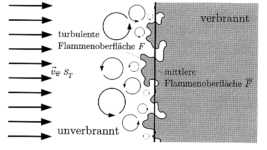
Abbildung 3.3-20: Turbulente Auffaltung der
Flammenoberfläche
In Experimenten wie auch im praktischen Motorbetrieb wird
jedoch eine degressive Abhängigkeit der turbulenten Brenngeschwindigkeit von
der Turbulenzintensität beobachtet. Es ist davon auszugehen, daß neben der rein geometrischen Flächenvergrößerung, die
von Damköhler als linear mit der Turbulenzintensität steigend angenommen wurde,
weitere Effekte wie die lokale Beeinflussung der laminaren Brenngeschwindigkeit
zu berücksichtigen sind.
Eine Verbesserung des Damköhlerschen
Ansatzes konnte in der Form
Gleichung 3.3-38: 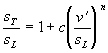
angegeben werden. Hier wird die degressive Abhängigkeit
durch den Exponenten n wiedergegeben,
der Werte von 0.4 < n < 1
annimmt.
Willms [xxiv][20]
und Trautwein et al. [xxv][9][1]
haben auf die stark instationäre Entwicklung von sT am Anfang der
Verbrennung hingewiesen. Ein Wert gemäß Gleichung 3.3-38 liegt danach nicht vom Anfang
der Verbrennung an vor. Die turbulente Flammengeschwindigkeit wächst zunächst
an und nähert sich dann asymptotisch diesem Endwert. Für die Bewertung der in
der Literatur angegebenen Beziehungen ergibt sich damit die Notwendigkeit zu
prüfen, in welcher Phase der Verbrennung die experimentellen Daten gewonnen
wurden.
Eine Möglichkeit, sT aus Experimenten zu ermitteln, bietet der
Ansatz 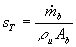 aus der Kontinuitätsgleichung. Hier ist
aus der Kontinuitätsgleichung. Hier ist 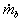 die Massenumsatzrate, ru die Dichte des
unverbrannten Gases und Ab
die mittlere turbulente Flammenfläche.
die Massenumsatzrate, ru die Dichte des
unverbrannten Gases und Ab
die mittlere turbulente Flammenfläche.
Von Bielert et al. [xxvi][21],[xxvii][22] wurde eine Erweiterung der Gleichung 3.3-38 vorgeschlagen, welche auch
die beobachtete zeitliche Entwicklung nach der Zündung als Näherung beschreibt
Gleichung 3.3-39: 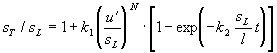 .
.
Die Koeffizienten k1,
k2 und l in Gleichung 3.3-39 sind zunächst nicht bekannt
und müssen aus dem Vergleich mit experimentell ermittelten Daten bestimmt
werden. Mit folgenden Werten konnten Rechnungen mit einem Front Tracking
Verfahren eine gute Übereinstimmung mit ca. 150 Versuchen erzielen
Gleichung 3.3-40: 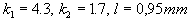 .
.
Eine Auswertung von Gleichung 3.3-39 für konstantes sL und
u' zeigt das exponentielle Anwachsen
von sT/sL
über der Zeit und die Annäherung an einen Grenzwert entsprechend Gleichung 3.3-38 in Abbildung 3.3-21. Bei Versuchen mit
Kompression kann die Turbulenzintensität in der Tat als weitgehend konstant
angenommen werden, während jedoch der Druck- und Temperaturanstieg die laminare
Flammengeschwindigkeit ändern. Ein Vergleich der turbulenten Flammengeschwindigkeit
zwischen Umsatzrechnung und Modellierung gemäß Gleichung 3.3-39 ist in Abbildung 3.3-30 dargestellt und im
Zusammenhang mit einem Front Tracking Verfahren zur Berechnung des
Motorprozesses diskutiert.
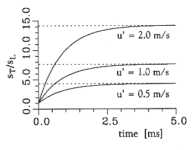
Abbildung 3.3-21: Verlauf des Verhältnisses von
turbulenter zu laminarer Flammengeschwindigkeit entsprechend Gleichung 3.3-38 bei Annahme konstanter
laminarer Geschwindigkeit sL und jeweils konstanter Turbulenz u'
3.3.3.8
Die Flammenflächendichte
Die Beschreibung des Verbrennungsvorganges in turbulenten
Strömungen basiert auf der Einteilung der Prozesse in unterschiedliche Regime
(s. Abbildung
3.3-19).
Die motorische Verbrennung kann in einem großen Bereich in das „flamelet regime" eingeordnet
werden. Hier wird angenommen, daß die Turbulenz die
Flamme zu einer dicken Zone faltet, wobei jedoch die laminare Flammenfläche
weiter existiert [xxviii][23],[xxix][24].
Aus dieser Annahme folgt, daß das lokale Verhalten
dem einer laminaren Flamme entspricht. Der Umsatz 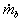 in der turbulenten Flammenzone ergibt sich
dann als Produkt aus der Dichte des unverbrannten Gases ru , der Oberfläche der gefalteten Flamme Al und der laminaren Flammengeschwindigkeit sL
in der turbulenten Flammenzone ergibt sich
dann als Produkt aus der Dichte des unverbrannten Gases ru , der Oberfläche der gefalteten Flamme Al und der laminaren Flammengeschwindigkeit sL
Gleichung 3.3-41: 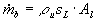 .
.
Die Flammenflächendichte S ist als ensemble-gemittelter
Quotient aus der Oberfläche dAl einer gefalteten Flamme in einem bilanzierten
Volumen und der Größe dV
des Volumens definiert (Marble et al. [xxx][25], Trouvé
et al. [xxxi][26], Duclos
et al. [xxxii][27]
Gleichung 3.3-42: 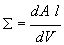 .
.
Für die Variable S läßt sich eine
Transportgleichung aufstellen, welche den differentiellen Gleichungen für die
Erhaltung von Masse, Impuls, Energie und Stoffmasse formell entspricht. Ihre
direkte Verbindung zum Massenumsatz durch die „flamelet"-Annahme
ersetzt die aufwendige Berechnung der reaktionskinetischen Bilanzgleichungen.
3.3.3.9
Messung der Flammenflächedichte
Die Eigenstrahlung der turbulenten Flammenzone auf der
CH-Bande wird ortsaufgelöst mit Hilfe einer CCD-Kamera zu unterschiedlichen
Zeiten quantitativ registriert. Auf Grund der ebenen, zweidimensionalen
Flammengeometrie im Einhubtriebwerk kann unmittelbar
zwischen Frischgas, Flammenzone und Abgas unterschieden werden. Die Auswertung
der Aufnahmen basiert auf der Annahme, daß die pro
Volumen emittierte Strahlung i(x,y) zum Massenumsatz 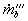 in
diesem Volumen proportional ist [xxxiii][28],[xxxiv][29]
in
diesem Volumen proportional ist [xxxiii][28],[xxxiv][29]
Gleichung 3.3-43: 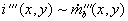
Diese Annahme konnte durch Vergleich der Gesamtemission mit
dem Umsatz aus einem thermodynamischen Modell verifiziert werden [xxxv][28].
Aus den bekannten globalen Größen von Gesamtemission Ifl und Umsatz 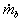 kann aus der lokalen Emission pro
Volumeneinheit i''' der lokale Umsatz
pro Volumen
kann aus der lokalen Emission pro
Volumeneinheit i''' der lokale Umsatz
pro Volumen 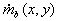 bestimmt
werden
bestimmt
werden
Gleichung 3.3-44: 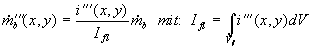 .
.
Im „flamelet regime"
läßt sich dann der Massenumsatz in die
Flammenflächendichte S umrechnen
Gleichung 3.3-45: 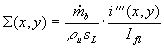 .
.
Zwischen der Flammenflächendichte S und dem
charakteristischen Faltungsmaß lT als mittlerem Abstand zwischen den
Reaktionszonen besteht folgender Zusammenhang
Gleichung 3.3-46: 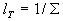 .
.
Der Umsatz in der Flammenzone läßt
sich in die turbulente Flammengeschwindigkeit sT aus der Dichte des
unverbrannten Gases ru und der mittleren
Fläche der Flammenzone Ab
umrechnen. Diese Größe läßt sich durch Integration
der Flammenflächendichte über ein Profil durch die Flammenzone ausdrücken, wo p die Koordinate senkrecht zur mittleren
Flammenfläche ist
Gleichung 3.3-47: 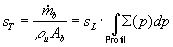 .
.
Aus einer Auswertung von Versuchen mit Azethylen-Luft-Gemischen
mit laminaren Flammengeschwindigkeiten von sL=0.64 m/s (Abbildung 3.3-22) und 1.3 m/s sowie
unterschiedlichen Turbulenzintensitäten von u'=0.5,
1.0, 2.0 m/s ergab sich der in Abbildung 3.3-23 dargestellte Zusammenhang
zwischen der Dicke der Flammenzone und dem Verhältnis von turbulenter zu
laminarer Ausbreitungsgeschwindigkeit [xxxvi][30].
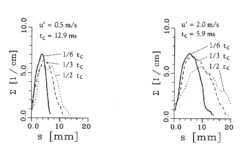
Abbildung 3.3-22: Profile der Flammenflächendichte
ermittelt aus Aufnahmen der CH-Bandenstrahlung für C2H2, sL=0.64
m/s mit verschiedenen Meßzeitpunkten und
Turbulenzintensitäten u', tC ist die Brenndauer
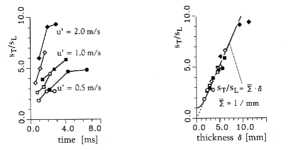
Abbildung 3.3-23: Verhältnis von turbulenter zu
laminarer Flammengeschwindigkeit über der Zeit (links) und über der Dicke der
Flammenzone (rechts) für C2H2 mit sL=0.64 m/s als
gefüllte Symbole und sL=1.3
m/s als offene Symbole
Der lineare Zusammenhang der in Abbildung 3.3-23 rechts dargestellten Größen (sT/sL)
und Flammendicke d weist darauf hin, daß das
effektive Faltungsmaß der Flamme bei den untersuchten Prozessen weitgehend
konstant ist, d.h. von u', von sL und
von der Zeit t weitgehend unabhängig
ist. Die Erhöhung des Umsatzes erfolgt also nicht über eine Erhöhung der Faltungsdichte sondern im wesentlichen über eine entsprechende Dickenzunahme
der Flamme. Für die aufgetragenen Größen gilt
Gleichung 3.3-48: 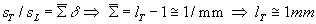 .
.
Aus dieser Beobachtung muß
gefolgert werden, daß der maximale Wert der
Flammenflächendichte im wesentlichen
von der Größe der turbulenten Strukturen festgelegt wird und wenig von der
Intensität der Turbulenz u' abhängt.
Auch bei frühen Beobachtungszeitpunkten (einem sechstel
der Brenndauer) liegt bereits dieses Faltungsmaß vor. Mit der Turbulenz steigt
die Dicke der Flammenzone, so daß die turbulente
Flammengeschwindigkeit entsprechend zunimmt. Eine ähnliche Beobachtung wurde
von Beretta, Rashadi und Keck [xxxvii][31] 1983
gemacht: Das aus Schlierenaufnahmen ermittelte
mittlere Faltungsmaß der turbulenten Flammenzone war ebenfalls für den
untersuchten Betriebszustand des Motors zeitlich konstant.
3.3.3.10
Berechnung der Flammenflächendichte
Die im folgenden durchgeführte
Modellierung hat die Aufgabe, die wesentlichen Effekte für Produktion
und Vernichtung von Flammenfläche zu erschließen und die turbulente
Flammengeschwindigkeit daraus zu ermitteln. Der Vergleich der Rechnung mit der
Auswertung der CH-Banden Messungen ermöglicht erstmals eine detaillierte
Kontrolle der Simulation.
Der Transport der Flammenflächendichte S wird durch folgende
Gleichung beschrieben 25,26, in der die Terme für
Produktion PS und
Auslöschung AS durch
Modelle zu definieren sind. Eine Diskussion unterschiedlicher Ansätze findet
man bei Duclos [xxxviii][27].
Gleichung 3.3-49: 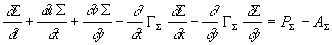
3.3.3.11
Das „Coherent Flame Model“
Die Gleichung
3.3-49
enthält Produktions- und Auslöschungsterme der Flammenfläche, welche im folgenden beschrieben werden. Die
sich daraus ergebende Transportgleichung für die Flammenflächendichte wurde von
Marble 1977 eingeführt und von Candel, Duclos, Poinsot und Trouvé [xxxix][26],[xl][27],[xli][32],[xlii][33] als „Coherent Flame Model" erweitert.
Die räumlichen Gradienten der zeitlich gemittelten
Gasgeschwindigkeit bewirken eine Deformation der laminaren Flammenoberfläche
Gleichung 3.3-50: 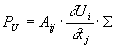
Die Gradienten der Grundströmung haben unter motorischen
Bedingungen eine Größenordnung von 500 s-1 in der Mitte der Flammenzone.
Zu den Rändern hin nimmt der Gradient auf Null ab. In
den hier vorgestellten Rechnungen werden Duclos et
al. 27 folgend alle Einträge der
Matrix Aij
zu Eins gesetzt.
Die stochastischen, turbulenten Schwankungen der
Gasgeschwindigkeit falten die laminare Flamme und erhöhen die
Flammenflächendichte. Die Höhe der Produktion wird abhängig vom integralen
Zeitmaß der Turbulenz Tt=k/e ausgedrückt als 32
Gleichung 3.3-51: 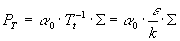 .
.
Der Kehrwert von Tt hat Werte zwischen
100 und 500 s-1. Die charakteristische Zeit Tt der Turbulenz ist
bei Annahme homogener Turbulenz unabhängig vom Ort. Für den Faktor a0 wurde bei der Rechnung mit
dem CFM der Wert 40 benutzt, um mit dem Experiment vergleichbare Werte für den
Umsatz zu erhalten. Dieser Wert liegt wesentlich höher als die in der Literatur
gefundenen Werte. Von Duclos werden für a0 Werte zwischen 1 und 2
eingesetzt [xliii][27],[xliv][32].
Konkave Strukturen der Reaktionszonen, wie sie an der
Hinterkante der Flamme überwiegend vorliegen, verringern ihre Oberfläche sehr
schnell. Diese starke Abnahme von Flammenfläche an der Hinterkante der
Flammenzone wird im CFM erfaßt durch einen Ansatz der
Form
Gleichung 3.3-52: 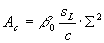 .
.
An Stellen gleicher Flammenflächendichte kann in dieser
Formulierung die Abnahme von Flammenfläche an der Vorderkante (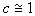 )
gegenüber der an der Hinterkante (
)
gegenüber der an der Hinterkante (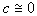 )
vernachlässigt werden. Für den Faktor b0
wird in den hier präsentierten Rechnungen der Wert 1.5 benutzt [xlv][27].
)
vernachlässigt werden. Für den Faktor b0
wird in den hier präsentierten Rechnungen der Wert 1.5 benutzt [xlv][27].
Die turbulenten Schwankungen der Gasgeschwindigkeit
deformieren nicht nur die Flamme, sondern bewirken auch einen diffusiven
Transport von Flammenfläche. Dieser Transport, welcher auf der linken Seite von
Gleichung
3.3-49
aufgeführt wurde, wird durch den Term erfaßt
Gleichung 3.3-53: 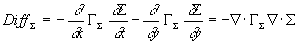 .
.
Der Diffusionskoeffizient GS wird aus folgender Gleichung bestimmt
Gleichung 3.3-54: 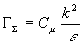 .
.
In dieser Gleichung kann die turbulente Energie k aus der herrschenden
Turbulenzintensität bestimmt werden, während die turbulente Dissipation
abgeschätzt werden muß oder aus der Annahme eines
turbulenten Längenmaßes lt bestimmt werden
kann [xlvi][34]
Gleichung 3.3-55: 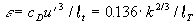
Der Parameter cD hat den Wert 0.37 [xlvii][35]. Im
motorischen Bereich wird allgemein angenommen, daß
das integrale Längenmaß lt mit der lichten
Brennraumhöhe im OT HOT zu
lt=0.2
HOT=4 mm abgeschätzt
werden kann [xlviii][34].
Die Krümmung der Flammenflächendichte erreicht an der Vorderkante ausgebildeter
Flammen Werte um 106 m-2, so daß
der Einfluß der Diffusion bei 102 s-1
liegt und den bisher beschriebenen Termen vergleichbar ist. Die Diffusion führt
zu einer Produktion an der Vorderkante und einem Rückgang von Flammenfläche im
Bereich des Maximums der Verteilung.
Bei Rechnungen mit den Termen Gleichung 3.3-50, Gleichung 3.3-51 und Gleichung 3.3-52 erhält man mit Aij=lij
und b0 =1.5 folgende
Grundgleichung für das „Coherent Flame Model"
Gleichung 3.3-56: 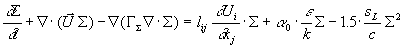
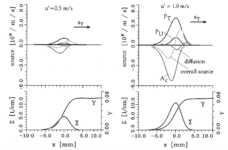
Abbildung 3.3-24: Profile der Quellterme des CFM für
niedrige (links) und mittlere (rechts) Turbulenzintensität. Der obere Teil
zeigt die Profile der verschiedenen Produktions- bzw. Auslöschungsterme der
Transportgleichung für die Flammenflächendichte, der untere Teil zeigt die
Profile der Flammenflächendichte S und des Brennstoffanteils Y .
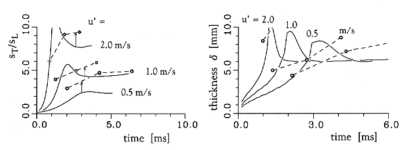
Abbildung 3.3-25: Vergleich CFM und Messung:
Zeitliche Entwicklung des Verhältnisses von turbulenter zu laminarer
Flammengeschwindigkeit links und Dicke der turbulenten Flammenzone rechts für C2H2 , l=1.8 , sL=0.65
m/s
In Abbildung
3.3-24
sind die Profile der einzelnen Terme im Bereich der Flammenzone dargestellt.
Die gepunktete Linie stellt die Summe der Quellen auf der rechten Seite von Gleichung 3.3-49 inklusive der Diffusion nach Gleichung 3.3-53 dar. Die links dargestellte
Rechnung wurde mit niedriger (u'=0.5
m/s) und die rechts dargestellte mit mittlerer (u'=1.0 m/s) Turbulenz durchgeführt. Die Profile wurden jeweils in
Phasen quasistationärer Ausbreitung der Flammenzone ermittelt.
In Abbildung
3.3-25
wird ein Vergleich globaler Größen zwischen Messung und Rechnung mit dem CFM
für niedrige, mittlere und hohe Turbulenz gezeigt. Abhängig von der
Turbulenzintensität stellt sich bei niedriger Turbulenz nach ca. 4 ms, bei mittlerer nach 3 ms und
bei hoher nach 2 ms ein quasistationärer Zustand der
Flammenzone ein.
Ein wesentlicher Unterschied zwischen Rechnung und Messung
liegt im qualitativen Verlauf der Flammendicke und dem Wert der maximalen
Faltung: Während die Dicke in der Messung mit steigender Turbulenz zunimmt, ist
der stationäre Wert der Dicke in der Rechnung unabhängig von der
Turbulenzintensität. Die Zunahme der turbulenten Flammengeschwindigkeit
entsteht durch eine immer stärkere Faltung. Im Experiment hingegen bleibt die
maximale Faltung innerhalb der Flammenzone im wesentlichen
gleich (s. Abbildung
3.3-22).
Eine weitere Diskrepanz zwischen der Rechnung und der
Messung ist in Abbildung
3.3-25
zu erkennen: Während sT/sL
der Rechnung mit u'=0.5 m/s erheblich
zu klein ist, ist diese Abweichung bei u'=2.0
m/s deutlich niedriger. Dies bedeutet, daß sT/sL
der Rechnung zu stark mit u'
ansteigt. Würde der Parameter a0
in Gleichung
3.3-51
aber gesenkt, würden die errechneten Werte für sT/sL noch niedriger ausfallen.
Aus diesen Überlegungen muß gefolgert werden, daß eine Produktion von Flammenfläche für niedrige
Turbulenzintensitäten oder eine turbulenzunabhängige Produktion nicht erfaßt ist. Die beiden beschriebenen Diskrepanzen zwischen
den Messungen und der Rechnung machen eine Erweiterung des CFM erforderlich.
3.3.3.12
Die Erweiterung des „Coherent Flame Model“
Eine Konditionierung der Gleichung 3.3-51 kann die Produktion
verringern, wenn sich der Abstand der Reaktionszonen lT einem Grenzwert lmin
nähert, welcher kleiner als das integrale Längenmaß lt
Gleichung 3.3-57: 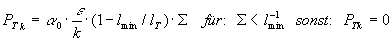
Hierdurch soll das Unterschreiten des mittleren Abstandes
der Reaktionszonen lmin
und somit das Anwachsen der Flammenflächendichte über den Wert 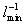 hinaus verhindert werden.
hinaus verhindert werden.
Konvexe Strukturen der Reaktionszonen an der Vorderkante der
Flamme breiten sich relativ zum Gas mit der laminaren Flammengeschwindigkeit sL aus
und vergrößern die Flammenoberfläche. Die Geschwindigkeit sL beträgt z.B. bei
Verbrennung eines stöchiometrischen Propan-Luft-Gemisches ungefähr 0.6 m/s und
kommt damit in einer zur turbulenten Schwankungsgeschwindigkeit u' vergleichbaren Größenordnung. Diese
Produktion wird vom CFM nicht berücksichtigt. Diese Inkonsistenz wurde bereits
von Trouvé [xlix][26][1]
herausgestellt
Gleichung 3.3-58: 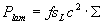 .
.
Dieser Term hat großen Einfluß an
der Vorderkante und fällt mit abnehmendem c.
Im Vergleich zu den bisher aufgeführten Termen ist das Produkt sL c² ungefähr um den Faktor 500 kleiner.
Weiterhin ist zu berücksichtigen, daß die Werte von S
an der Vorderkante klein sind. Wählt man als Abschätzung 1/10 des Maximums, so
folgt, daß der Faktor f die Größenordnung 5000 haben muß. Die
Rechnungen legen einen Wert von f=1.700
nahe. Die Überlagerung des Vernichtungsterms gemäß Gleichung 3.3-52 und der Produktion (Gleichung 3.3-58) bewirkt einen
Vorzeichenwechsel, wie er auch von Trouvé [l][26]
n direkten numerischen Simulationen gefunden wurde.
Hierdurch ergibt sich folgende Transportgleichung für die
Flammenfläche
Gleichung 3.3-59: 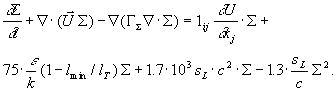
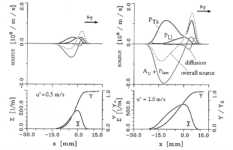
Abbildung 3.3-26: Profile der Quellterme des
erweiterten CFM für niedrige (links) und mittlere (rechts) Turbulenzintensität
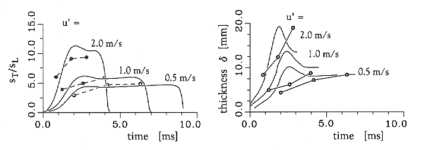
Abbildung 3.3-27: Vergleich zwischen erweitertem CFM
und Messung: Zeitliche Entwicklung des Verhältnisses von turbulenter zu
laminarer Flammengeschwindigkeit (links) und der Dicke der turbulenten
Flammenzone (rechts) für drei unterschiedliche Turbulenzintensitäten
Die Abbildung
3.3-26
und Abbildung
3.3-27
zeigen die Ergebnisse der Rechnungen mit Gleichung 3.3-59 in der gleichen Art wie zuvor
die Ergebnisse des CFM. Abweichend wurden jedoch in Abbildung 3.3-26 Ergebnisse der Rechnung mit u'=2.0 m/s dargestellt.
Die Konditionierung der Produktion durch Turbulenz PT bewirkt wie erwartet die Zunahme
der Flammendicke bei steigender Turbulenz. Die maximale Faltung nimmt von u'=0.5 m/s bis 2.0 m/s nur leicht zu. Um
ein mit dem Experiment vergleichbares Maximum der Faltung zu erhalten, wurde lmin
=1.2 mm gesetzt.
Abbildung
3.3-27
zeigt, daß durch Einführung des turbulenzunabhängigen
Produktionsterms (Gleichung
3.3-58)
eine bessere Übereinstimmung des Verhältnisses von turbulenter zu laminarer
Flammengeschwindigkeit sT/sL
erreicht wurde.
Durch die Erweiterung des CFM konnten die wesentlichen
Diskrepanzen zwischen der Rechnung und der Messung der Flammenflächendichte
eliminiert werden.
3.3.3.13
Simulation des gesamten Verbrennungsprozesses
Zur Simulation des gesamten, mehrdimensionalen
Verbrennungsvorgangs im Einhubtriebwerk wird an Front
Tracking Verfahren angeknüpft, wie sie in [li][36],[lii][37],[liii][38],[liv][39]
dargestellt wurden. In diesen Arbeiten wird eine unendlich dünne laminare
Flammenfläche verfolgt und ihre Faltung durch die Turbulenz mit dem Random
Vortex Verfahren [lv][40],[lvi][41],[lvii][42] , also eine Überlagerung der Grundströmung mit
zufallsverteilten Wirbeln, realisiert. In der vorliegenden Arbeit wird dagegen
das Fortschreiten der turbulenten Flamme als Zone mit gleichmäßig verteiltem
Reaktionsumsatz betrachtet, ohne ihre Struktur im Detail aufzulösen. Bei diesem
Vorgehen wird berücksichtigt, daß die turbulente
Flammengeschwindigkeit eine Funktion der Turbulenzintensität und der Zeit ist. Desweiteren hat die Reaktionszone eine endliche Dicke und
kann nicht als Unstetigkeit aufgefaßt werden.
Das in [lviii][43],[lix][22][1]
vorgestellte Front Tracking Verfahren mit den beschriebenen Modellannahmen
wurde zur Simulation der Verbrennungsvorgänge in einem Einhubtriebwerk
angewandt. Die numerische Simulation dient der Interpretation der im Einhubtriebwerk gewonnenen experimentellen Daten, während
die Versuchsergebnisse eine Kontrolle der Simulation erlauben und eine
Anpassung benötigter Parameter ermöglichen. Die Simulation benötigt als einzige
gemessene Eingabegröße den Weg-Zeit-Verlauf des Kolbens. Die turbulente
Flammengeschwindigkeit wird gemäß Gleichung 3.3-38 vorgegeben.

Abbildung 3.3-28: Vergleich von Schlierenaufnahmen
[lx][7][1]
mit der numerischen Simulation für: C3H8, l=1.0, u'=0.74 m/s, die Zündung erfolgte bei t=0.0 ms
3.3.3.14
Flammenkonturen
Ein Vorteil des Front Tracking gegenüber anderen Methoden
mit quasi-dimensionalen thermodynamischen Modellen liegt darin, daß keine Kontur der Flammenzone vorgegeben werden muß. Stattdessen entwickelt sich die Kontur im Laufe der
Berechnung unter dem Einfluß des Strömungsfeldes und
der Verbrennung. Die zeitliche Entwicklung dieser Flammenkonturen soll hier mit
experimentellen Ergebnissen verglichen werden. Trautwein [lxi][7][1]
hat den Verbrennungsvorgang im Einhubtriebwerk für
verschiedene Brennstoffe und verschiedene Turbulenzintensitäten mit
kinematographischen Schlierenaufnahmen untersucht.
In Abbildung
3.3-28
sind Filmaufnahmen der zeitlichen Entwicklung der Flammenzone (links) den
numerisch ermittelten Flammenkonturen (rechts) gegenübergestellt. In der
Simulation sind Außen- und Innenkontur der Flammenzone sowie das aktuelle
Strömungsfeld dargestellt.
Das Bild bezieht sich auf eine
stöchiometrische Propan/Luft Mischung mit mittlerer Turbulenzintensität
(u'= 0.74). Es steht repräsentativ
für eine ganze Reihe von Bildsequenzen, die in
7,21 für weitere Luftverhältnisse
und auch für Azethylen wiedergegeben werden.
Allgemein ist festzustellen:
· Die Verbrennung
verläuft mit zunehmender Turbulenz schneller.
· Die Dicke der
Flammenzone wächst mit der Turbulenz bei gegebener Position.
· Die Dicke der
Flammenzone wächst mit der Zeit bei gegebener Turbulenzintensität.
3.3.3.15
Flammendicke
Eine Auswertung der Schlierenbilder
ermöglicht die Bestimmung der Flammenzonendicke als Funktion des Volumenanteils
yb.
Diese Auswertung wurde von Trautwein in [lxii][7][1]
durchgeführt. In Abbildung
3.3-29
sind die Ergebnisse dieser Auswertung den Ergebnissen der numerischen
Simulation gegenübergestellt.
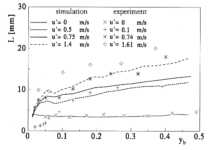
Abbildung 3.3-29: Wachstum der Flammenzonendicke bei
verschiedenen Turbulenzintensitäten für C3H8, l=1
Es ist zu erkennen, daß die Dicke
der Flammenzone zunächst relativ schnell auf einen Wert wächst, der sich dann
aber im Laufe der weiteren Verbrennung nur noch wenig ändert. Dieser Endwert
der Flammenzonendicke wächst mit zunehmender Turbulenzintensität.
3.3.3.16
Turbulente Flammengeschwindigkeit
Bei der Modellierung des Strömungsfeldes wurde die hier
benutzte Gleichung
3.3-38
für die turbulente Flammengeschwindigkeit verwendet, die das zeitabhängige
Anwachsen dieser Größe berücksichtigt. Die benutzten Koeffizienten für eine
stöchiometrische Propan-Luft-Mischung sind: k1
= 4.3 , k2
= 1.7 , l =
0.95 mm, N = 1.0 .
Über eine Umsatzrechnung läßt sich aus dem gemessenen
Druckverlauf ebenfalls sT
bestimmen (s.[lxiii][7],[lxiv][10],[lxv][21]).
Die Genauigkeit der Bestimmung über die Umsatzrechnung ist abhängig von der
Genauigkeit, mit der die mittlere Flammenfläche Ab bestimmt werden kann. Bis zum Kolbenkontakt ist
dieses relativ problemlos möglich, danach wird die Bestimmung infolge der
schleifenden Schnitte an der Wand und der Vernachlässigung der
Flammenzonendicke jedoch ungenau.
In Abbildung
3.3-30
sind die aus der Umsatzrechnung berechnete turbulente Flammengeschwindigkeit
als durchgezogene Linien und die in der numerischen Simulation verwendete
turbulente Flammengeschwindigkeit nach Gleichung 3.3-39 als gestrichelte Linien über
der Zeit für ein stöchiometrisches Propan-Luft-Gemisch und verschiedene
Turbulenzintensitäten aufgetragen.
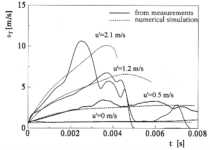
Abbildung 3.3-30: Einfluß
der Turbulenzintensität auf die turbulente Flammengeschwindigkeit für C3H8,
l=1
Die turbulente Flammengeschwindigkeit steigt mit der Zeit
zunächst stark an. Bei Annäherung an den asymptotischen Endwert wird dieser
Anstieg flacher. Die turbulente Flammengeschwindigkeit folgt jetzt nur noch dem
Verlauf der laminaren Flammengeschwindigkeit, die abhängig von Druck und
Temperatur variiert. In der Phase steigenden Druckes wächst die turbulente
Flammengeschwindigkeit somit weiter und fällt erst in der Expansionsphase am
Ende der Verbrennung mit dem abnehmenden Druck. Mit zunehmender Turbulenzintensität
läuft die Verbrennung schneller ab, die Kurven der turbulenten
Flammengeschwindigkeit werden steiler und erreichen höhere Werte. Während die
Kurven aus der numerischen Simulation glatt verlaufen, zeigt sich in den Kurven
aus der Umsatzrechnung der Einfluß der geometrischen
Annahmen. Bei dem ersten Kolbenkontakt der Flamme steigen diese Kurven bedingt
durch eine Unterschätzung der Flammenfläche zunächst steil an. In einer
späteren Phase wiederholt sich dieser Anstieg beim Kontakt der Flamme mit den
Seitenwänden. Für den Vergleich der Kurven sollte daher nur der erste Teil der
Kurven bis zu der ersten Überhöhung betrachtet werden. In diesem Bereich ist
die Übereinstimmung der Kurven für alle untersuchten Turbulenzintensitäten gut.
3.3.3.17
Einfluß der Turbulenzintensität
In Abbildung
3.3-31
ist der Einfluß der Turbulenzintensität auf den
Verbrennungsablauf für C3H8, l=1 dargestellt. Im oberen Teil ist der gemessene Druckverlauf als
durchgezogene Linie dem berechneten Druckverlauf als gestrichelte Linie gegenüber gestellt. Im unteren Teil werden die
Volumenanteile yb,
wie sie aus der Umsatzrechnung ermittelt wurden (durchgezogene Linien) mit den
entsprechenden Daten aus der Simulation (gestrichelte Linien) verglichen.

Abbildung 3.3-31: Einfluß
der Turbulenzintensität auf den Verbrennungsvorgang für C3H8,
l=1
Es zeigt sich ein deutlicher Einfluß
der Turbulenzintensität. Mit zunehmender Turbulenzintensität steigt der
Maximaldruck und die Verbrennung läuft schneller ab, das heißt die Druckmaxima
werden früher erreicht und die Brennfunktion yb steigt schneller
an. In der Anfangsphase der Verbrennung weichen die Kurven zwar etwas
voneinander ab, aber der qualitative Verlauf einschließlich der Wendestellen
wird gut wiedergegeben. Die Kurven für den Volumenanteil des Verbrannten zeigen
ebenfalls eine gute Übereinstimmung.
3.3.3.18
Einfluß des Kompressionsverhältnisses
Für ein stöchiometrisches Propan-Luft-Gemisch liegen
experimentelle Daten über den Einfluß des
Verdichtungsverhältnisses auf den Verbrennungsvorgang im Einhubtriebwerk
unter laminaren Bedingungen, also ohne Einsatz des Turbulenzgenerators, vor [lxvi][10],[lxvii][21].
In Abbildung
3.3-32
werden diese Daten mit den Ergebnissen der numerischen Simulation verglichen.
Mit zunehmendem Verdichtungsverhältnis steigt der Druck zum Zeitpunkt der
Zündung. Die Druckmaxima steigen ebenfalls an und verschieben sich nach vorn.
Die Brennfunktionen yb
steigen ebenfalls schneller an, jedoch ist der Einfluß
nur gering. Die numerische Simulation ist auch hier in der Lage, die Daten aus
dem Experiment hinreichend genau zu reproduzieren.
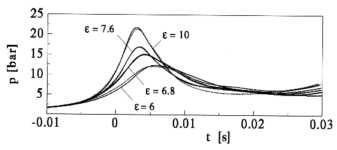
Abbildung 3.3-32: Einfluß
des Kompressionsverhältnisses auf den Verbrennungsvorgang für C3H8,
l=1 , u'=0 m/s
3.3.4 Zusammenfassung
Die Verbrennung im Ottomotor wird durch die turbulente Flammenausbreitung
bestimmt. Diese hängt einerseits von der laminaren Brenngeschwindigkeit und
andererseits von Turbulenzparametern wie der turbulenten
Schwankungsgeschwindigkeit und dem integralen Längenmaß ab. Diese Abhägigkeiten wurden in den Teilprojekten A3 und A5 des
Sonderforschungsbereiches sowohl experimentell wie theoretisch unter motornahen
Bedingungen untersucht. Dazu wurde ein Einhubtriebwerk
(A5) und ein Transparentmotor (A2) eingesetzt und lokale Flammenstrukturen
sichtbar gemacht, um deren Interaktion mit dem turbulenten Strömungsfeld zu
klären. Bei der theoretischen Beschreibung wurde die Bedeutung von
Interaktionslängen und der Flammenflächendichte besonders herausgearbeitet. Die
Geschwindigkeit der Flammenausbreitung bestimmt nicht nur den Ausbrand, sie hat auch unmittelbare Auswirkungen auf die im
folgenden Abschnitt behandelten Klopfphänomene in Ottomotoren. Erfolgt der Ausbrand des Endgases schnell
genug, kann Klopfen vermieden werden. Andererseits führen sehr schnelle
Ausbreitungsvorgänge zu einer schnellen Temperaturerhöhung auf Grund adiabater
Kompression im Endgas und können damit die
Klopfentstehung fördern.
3.3.5 Abbildungsverzeichnis
Abbildung 3.3-1: Schlierenaufnahmen
der Flammenausbreitung im Transparentmotor
Abbildung 3.3-2: Laminare Brenngeschwindigkeiten von iso-Oktan bei f=1.
Die Punkte stellen Berechnungen mit einem vollständigen kinetischen Mechanismus
dar, die durchgezogenen Linie die explizite Approximation.
Abbildung 3.3-3: Konzentrations- und Temperaturprofile in
der Reaktionszone
Abbildung 3.3-4: Darstellung des Brennraumes des Einhubtriebwerkes
Abbildung 3.3-5: Spektrale Energieverteilung, Abklingzeit
der Turbulenz tA=6
ms, ohne Kompression
Abbildung 3.3-6: RMS-Wert während der Kompression
Abbildung 3.3-7: Integrales Längenmaß während der
Kompression
Abbildung 3.3-8: Turbulente Längenmaße während der
Kompression eines geschleppten Ottomotors
Abbildung 3.3-9: Die turbulente Flammendicke und die
Taylor-Länge der Flammenstruktur
Abbildung 3.3-10: Interaktion einer laminaren Flammenfront
mit diskreten Wirbeln verschiedener Größenordnungen
Abbildung 3.3-11: Lokaler Einfluß
des Strömungsfeldes auf die laminare Brenngeschwindigkeit
Abbildung 3.3-12: Vergleich der berechneten und der
experimentellen Markstein Zahlen für Propan bei p=1bar und einer Vorwärmtemperatur von 298K (aus 6)
Abbildung 3.3-13: Optischer Aufbau für
Laser-Lichtschnittaufnahmen am VW-Transparentmotor
Abbildung 3.3-14: Anordnung von Laser-Lichtschnitt und
Bildbereich im Brennraum des VW-Transparentmotors
Abbildung 3.3-15: Turbulente Flammenfront bei der
Flammenausbreitung im Ottomotor
Abbildung 3.3-16: Spektrale Schwankungsdichte der räumlichen
Flammenstrukturen
Abbildung 3.3-17: Charakteristische Längenskalen der
turbulenten Flammenausbreitung im Ottomotor 17
Abbildung 3.3-18: Die Werte von v'/sL für die verschiedenen
Betriebspunkte
Abbildung 3.3-19: Phasendiagramm der vorgemischten
turbulenten Verbrennung
Abbildung 3.3-20: Turbulente Auffaltung der
Flammenoberfläche
Abbildung 3.3-21: Verlauf des Verhältnisses von turbulenter
zu laminarer Flammengeschwindigkeit entsprechend Gleichung 3.3-38 bei Annahme
konstanter laminarer Geschwindigkeit sL und jeweils konstanter Turbulenz u'
Abbildung 3.3-22: Profile der Flammenflächendichte ermittelt
aus Aufnahmen der CH-Bandenstrahlung für C2H2, sL=0.64
m/s mit verschiedenen Meßzeitpunkten und
Turbulenzintensitäten u', tC ist die Brenndauer
Abbildung 3.3-23: Verhältnis von turbulenter zu laminarer
Flammengeschwindigkeit über der Zeit (links) und über der Dicke der Flammenzone
(rechts) für C2H2 mit sL=0.64 m/s als
gefüllte Symbole und sL=1.3
m/s als offene Symbole
Abbildung 3.3-24: Profile der Quellterme des CFM für
niedrige (links) und mittlere (rechts) Turbulenzintensität. Der obere Teil
zeigt die Profile der verschiedenen Produktions- bzw. Auslöschungsterme der
Transportgleichung für die Flammenflächendichte, der untere Teil zeigt die
Profile der Flammenflächendichte S und des Brennstoffanteils Y .
Abbildung 3.3-25: Vergleich CFM und Messung: Zeitliche
Entwicklung des Verhältnisses von turbulenter zu laminarer
Flammengeschwindigkeit links und Dicke der turbulenten Flammenzone rechts für C2H2 , l=1.8 , sL=0.65
m/s
Abbildung 3.3-26: Profile der Quellterme des erweiterten CFM
für niedrige (links) und mittlere (rechts) Turbulenzintensität
Abbildung 3.3-27: Vergleich zwischen erweitertem CFM und
Messung: Zeitliche Entwicklung des Verhältnisses von turbulenter zu laminarer
Flammengeschwindigkeit (links) und der Dicke der turbulenten Flammenzone
(rechts) für drei unterschiedliche Turbulenzintensitäten
Abbildung 3.3-28: Vergleich von Schlierenaufnahmen 7 mit der numerischen Simulation für:
C3H8, l=1.0, u'=0.74 m/s, die Zündung erfolgte bei t=0.0 ms
Abbildung 3.3-29: Wachstum der Flammenzonendicke bei
verschiedenen Turbulenzintensitäten für C3H8, l=1
Abbildung 3.3-30: Einfluß der
Turbulenzintensität auf die turbulente Flammengeschwindigkeit für C3H8,
l=1
Abbildung 3.3-31: Einfluß der
Turbulenzintensität auf den Verbrennungsvorgang für C3H8,
l=1
Abbildung 3.3-32: Einfluß des
Kompressionsverhältnisses auf den Verbrennungsvorgang für C3H8,
l=1 , u'=0 m/s
3.3.6 Literatur
Webseite aktualisiert am 30.11.2000
[i][1] J. Warnatz: in „Combustion
Chemistry“ (W.C. Gardiner, Ed.), Springer-Verlag, Heidel-berg, S. 197ff.,
(1984)
[ii][2] N.
Peters, B. Rogg: in „Reduced Kinetic Mechanisms for Applications in Combustion Systems“ (N. Peters, B. Rogg, Eds.), Springer-Verlag,
Heidelberg, pp. 284-307, (1993)
[iii][3] C.M.
Müller, K. Seshadri, J.Y. Chen: „Reduced Kinetic Mechanisms for Counterflow
Methanol Diffusion Flames“, in „Reduced Kinetic
Mechanisms for Applications in Combustion Systems“ (N.
Peters, B. Rogg, Eds.), Springer-Verlag, Heidelberg, pp. 284-307, (1993)
[iv][4] K.
Seshadri, M. Bollig, N. Peters: „Numerical and Asymptotic Studies of the
Structure of Stoichiometric and Lean Heptane Flames“,
Combustion and Flame, (1996)
[v][5] H.
Pitsch, N. Peters, K. Seshadri: „Numerical and Asymptotic Studies of the
Structure of Premixed Iso-Octane Flames“, Twenty-Sixth
Symposium (International) on Combustion, (1996)
[vi][6] U.C.
Müller, M. Bollig, N. Peters: „Approximations for Burning Velocities and
Markstein Numbers for Lean Hydrocarbon Flames“,
Combustion and Flame, (1996)
[vii][7] S.E. Trautwein: „Untersuchung des Einflusses der Turbulenz auf die
Flammenausbreitung unter motorischen Bedingungen“, Dissertation, RWTH Aachen,
(1989)
([viii][8] G. Adomeit, S.E. Trautwein, A. Grudno:
„Untersuchung spezieller Aspekte der turbulenten Verbrennung in einem
Einhubtriebwerk“, Kolloquium des SFB 224 Motorische Verbrennung, Aachen, (1990)
[ix][9] S.E.
Trautwein, A. Grudno, G. Adomeit: „The Influence of Turbulence Intensity and
Laminar Flame Speed on Turbulent Flame Propagation Under Engine Like
Conditions“, 23rd Symposium (Int.) on Combustion, pp. 723-728, (1990)
[x][10] A. Grudno: „Untersuchung der turbulenten Flammenausbreitung unter
ottomotorischen Bedingungen“, Fortschr.-Ber. VDI Reihe 12 Nr.206, Düsseldorf:
VDI-Verlag, Dissertation, RWTH Aachen, (1994)
[xi][11] U. Renz, H. Hüppelshäuser, A. Schneemann, F. Lange: „Strömung und
Wärmeübergang im Zylinder eines geschleppten Motors“, Kolloquium des SFB 224
„Motorische Verbrennung“, RWTH Aachen, (1993)
[xii][12] H. Hüppelshäuser: „Experimentelle Untersuchung der Strömung und des
Wärmeübergangs im Kolbenmotor“, Dissertation, RWTH Aachen, (1992)
[xv][13] M. Oberlack: „Herleitung und Lösung einer Längenmaß- und
Dissipations-Tensorgleichung für turbulente Strömungen“, Dissertation, RWTH
Aachen, (1994)
[xvi][14] N.
Peters: „Laminar Flamelet Concepts in Turbulent Combustion“, Twenty-First
Symposium (International) on Combustion, The Combustion Institute, Pittsburgh,
s.1231-1250, (1986)
[xvii][15] P.
Clavin: „Dynamic Behaviour of Premixed Flame Fronts in Laminar and Turbulent
Flows“, Progr.Energy Combust. Sci.,11, 1-59, (1985)
[xix][16] S.C.
Taylor: Ph. D. thesis, University of Leeds (1991)
[xx][17] M. Wirth: „Die turbulente Flammenausbreitung im Ottomotor und ihre
charakteristischen Längenskalen“, Dissertation, RWTH Aachen, (1993)
[xxi][18] N.
Peters: „Spectral Closure for Premixed Turbulent Combustion in the Flamelet
Regime“, J. Fluid Mech., 242: p.611-630, (1992)
[xxiii][19] N.
Peters: „Length Scales in Laminar and Turbulent Flames in Numerical Approaches
to Combustion Modeling“, (S.Oran, J.P. Boris, Eds.), Progress in Astronautics
and Aeronautics 135, s.155-162, (1991)
[xxiv][20] H. Willms: „Untersuchung der Wechselwirkung zwischen
Strömungsfeld und Reaktionsfront beim deflagrativen Abbrand von
Kohlenwasserstoff-Luft-Gemischwolken“, Fortschr.-Ber. VDI Reihe 19 Nr. 27,
VDI-Verlag, Düsseldorf, Dissertation, RWTH Aachen, (1988)
[xxvii][21] U. Bielert: „Numerische Simulation turbulenter
Verbrennungsvorgänge unter motorischen Bedingungen mit einem Front Tracking
Verfahren“, Fortschr.-Ber. VDI Reihe 12 Nr. 223, Düsseldorf: VDI Verlag,
Dissertation, RWTH Aachen, (1994)
[xxviii][22] U.
Bielert, M. Klug, G. Adomeit: „Application of Front Tracking Techniques to the
Turbulent Combustion Processes in a Single Stroke Engine“, wird veröffentlich
in Combustion and Flame, (1996)
[xxix][23] H.
Naji, R. Said, R.P. Borghi: „Towards a General Turbulent Combustion Model for
Spark Ignition Engines“, SAE Technical Paper 890672, (1989)
[xxx][24] J.
Abraham, F.A. Williams, F.V. Bracco: „A Discussion of Turbulent Flame Structure
in Premixed Charges, SAE Technical Paper 850345, (1985)
[xxxi][25] F.E.
Marble, J.E. Broadwell: „The Coherent Flame Model for Turbulent Chemical
Reactions“, Project Squid Tech. Rep. TRW-9-PU, (1977)
[xxxii][26] A.
Trouvé, T. Poinsot: „The Evolution Equation for the Flame Surface Density in
Turbulent Premixed Combustion“, J. Fluid. Mech., Vol. 278, pp. 1-31,
(1994)
[xxxiii][27] J.M.
Duclos, D. Veynante, T. Poinsot: „A Comparison of Flamelet Models for Premixed
Turbulent Combustion“, Combustion and Flame 95: 101-117, (1993)
[xxxiv][28] A.D.
Grudno, S.E. Trautwein, H.J. Wassenberg, G. Adomeit: „Spatially Resolved
Determination of the Turbulent Flame Speed from CH Band Emission Measurements
Under Engine Conditions“, SAE Technical Paper 940685, (1994)
[xxxv][29] G. Adomeit, D.-H. Chung: „Untersuchung der molekularen
Geschwindigkeitsverteilung von Radikalen in chemischen Gasphasenreaktionen“,
Forschungsberichte des Landes NRW, Westdeutscher Verlag, (1978)
[xxxvii][30] H.
Wassenberg, A. Grudno, G. Adomeit: „Premixed Turbulent Flames at Engine
Conditions: Profiles of CH Band Emission across the Flame Zone Determining
Local Values of Burning Rate“, Int. Symp. on Transport Phenomena in Comb., San
Francisco, (1994)
[xxxviii][31] G.P.
Beretta, M. Rashadi, J.C. Keck: „Turbulent Flame Propagation and Combustion in
Spark Ignition Engines“, Combustion and Flame 52:217-245, (1983)
[xlii][32] D.
Veynante, J.M. Duclos, J. Piana, S. Candel: „Flame Surface Density Models for
Turbulent Combustion: Theory and Application“, Euro-Conference RWTH-Aachen,
Institut für Technische Mechanik, (1995)
[xliii][33] S.M.
Candel, T. Poinsot: „Flame Stretch and the Balance Equation for the Flame
Surface Area“, Comb. Sci.Tech. 70:1-50, (1990)
[xlvii][34] J.B.
Heywood: „Combustion Engine Fundamentals“, McGraw-Hill, (1988)
[xlviii][35] P.A.
Libby, F.A. Williams: „Laminar Flamelets in Turbulent Flames Turbulent Reacting
Flows“, pp. 63-112, Academic Press (1994)
[liii][36] W.T. Ashurst,
P.K. Barr: „Stochastic Calculation of Laminar Wrinkled Flame Propagation via
Vortex Dynamics“, Comb. Sci. and Tech. 34:227-256, (1983)
[liv][37] J.
Sethian: „Turbulent Combustion in Open and Closed Vessels“, Journ. of Comp.
Physics 54:425-456, (1984)
[lv][38] A.F.
Ghoniem, A.J. Chorin, A.K. Oppenheim: „Numerical Modeling of Turbulent
Combustion in Premixed Gases“, 18th Symp. (Int.) on Combustion, 1375-1320,
(1981)
[lvi][39] P.K.
Barr: „Acceleration of a Flame by Flame-Vortex Interactions“, Combustion and
Flame 82:111-125, (1990)
[lvii][40] A.J.
Chorin: „Flame Advection and Propagation Algorithms“, Journ. of Comp. Physics
25:253-272, (1977)
[lviii][41] A.J.
Chorin: „Random Choise Methods with Application to Reacting Gas Flow“, Journ.
of Comp. Physics 25:253-272, (1977)
[lix][42] A.J.
Chorin: „Random Choise Solution of Hyperbolic Systems“, Journ. of Comp. Physics
22:517-533, (1976)
[lx][43] U.
Bielert, M. Klug, G. Adomeit: „Numerical Simulation of the Turbulent Combustion
Process in a Rapid Compression Device“, SAE Technical Paper 940211, (1994)
zurück zur Startseite